国产小呦泬泬99精品,国产激情综合在线观看,欧美国产日韩A在线视频

　　炒股就看金麒麟分析師研報，權威，專業，及時，全面，助您挖掘潛力主題機會！

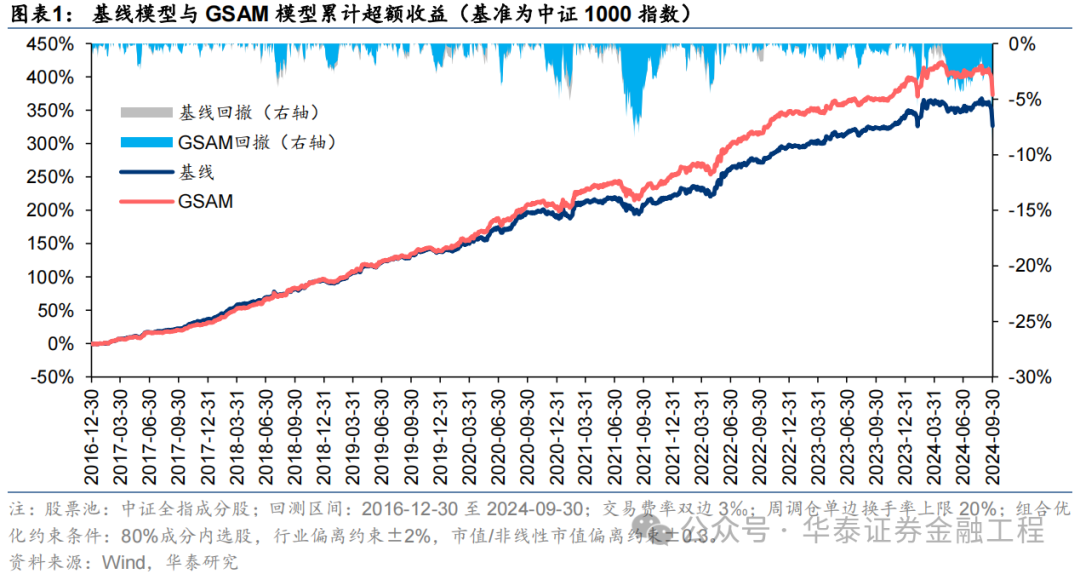
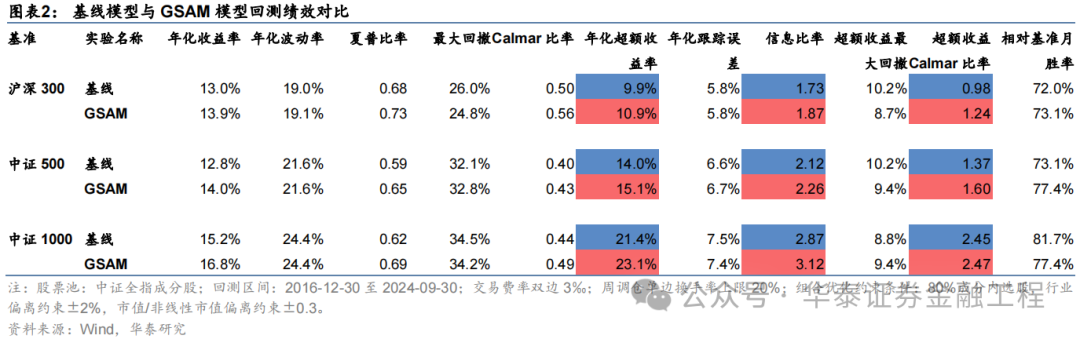
本研究介紹一種低成本、高通用性的正則化方法——Sharpness Aware Minimization（SAM），從優化器的角度提升模型的泛化性能。在GRU基線模型的基礎上，采用傳統優化器AdamW、SAM優化器及其四種改進版本進行對照實驗。結果表明應用SAM優化器能顯著提升模型預測因子的多頭端收益，且基于各類SAM模型構建的指數增強組合業績均顯著優于基線模型。其中，GSAM模型在三組指數增強組合上均取得良好表現，滬深300、中證500和中證1000增強組合年化超額收益分別為10.9%、15.1%和23.1%，信息比率分別為1.87、2.26和3.12，顯著優于基線模型，而ASAM模型2024年表現突出，三組指數增強組合超額收益均領先基線模型約5pct。

人工智能84：應用SAM優化器提升AI量化模型的泛化性能

SAM優化器通過追求“平坦極小值”，增強模型魯棒性

SGD、Adam等傳統優化器進行梯度下降時僅以最小化損失函數值為目標，易落入“尖銳極小值”，導致模型對輸入數據分布敏感度高，泛化性能較差。SAM優化器將損失函數的平坦度加入優化目標，不僅最小化損失函數值，同時最小化模型權重點附近損失函數的變化幅度，使優化后模型權重處于一個平坦的極小值處，增加了模型的魯棒性。基于SAM優化器，ASAM、GSAM等改進算法被陸續提出，從參數尺度自適應性、擾動方向的準確性等方面進一步增強了SAM優化器的性能。

SAM優化器能降低訓練過程中的過擬合，提升模型的泛化性能

SAM優化器設計初衷是使模型訓練時在權重空間中找到一條平緩的路徑進行梯度下降，改善模型權重空間的平坦度。可通過觀察模型訓練過程中評價指標的變化趨勢以及損失函數地形圖對其進行驗證。從評價指標的變化趨勢分析，SAM模型在驗證集上IC、IR指標下降幅度較緩，訓練過程中評價指標最大值均高于基線模型；從損失函數地形分析，SAM模型在訓練集上損失函數地形相較基線模型更加平坦，測試集上損失函數值整體更低。綜合兩者，SAM優化器能有效抑制訓練過程中的過擬合，提升模型的泛化性能。

SAM優化器能顯著提升AI量化模型表現

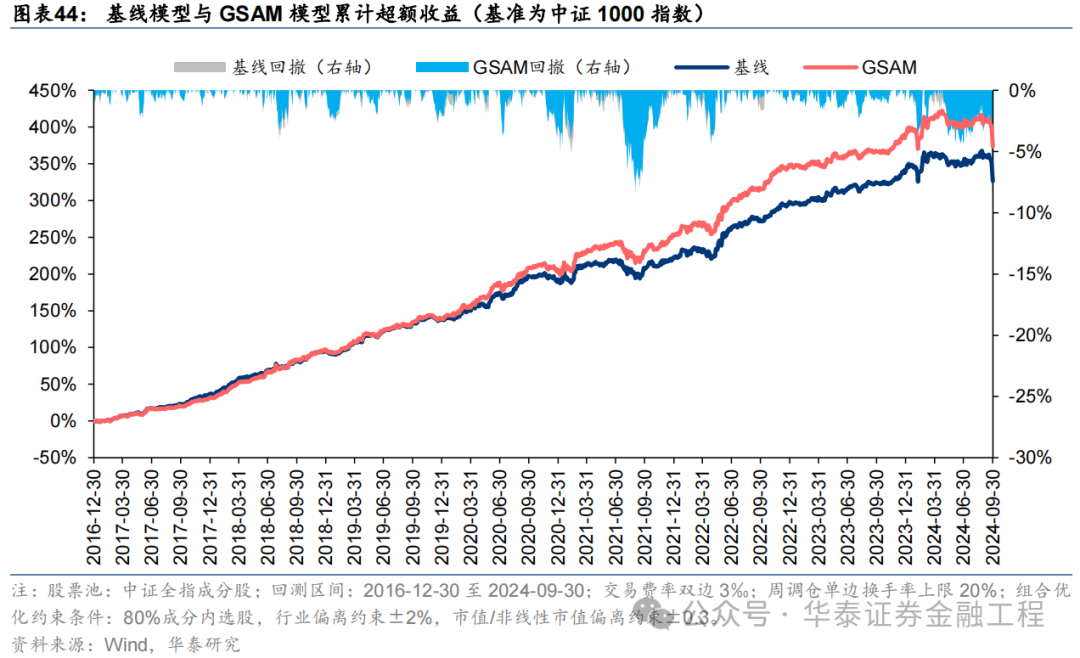
本研究基于GRU模型，對比AdamW優化器與各類SAM優化器模型表現。從預測因子表現看，SAM優化器能提升因子多頭收益；從指數增強組合業績看，SAM模型及其改進版本模型在三組指數增強組合業績均顯著優于基線模型。2016-12-30至2024-09-30內，綜合表現最佳模型為GSAM模型，單因子回測TOP層年化收益高于31%，滬深300、中證500和中證1000增強組合年化超額收益分別為10.9%、15.1%和23.1%，信息比率分別為1.87、2.26和3.12，顯著優于基線模型。2024年以來ASAM模型表現突出，三組指數增強組合超額收益均領先基線模型約5 pct。

01 導讀

提升泛化性能是增強AI量化模型表現的關鍵。對AI量化模型應用適當的正則化方法，可以進一步“強化”模型，提升其泛化性能，讓量化策略的表現更進一步。正則化方法的目標為引導模型捕捉數據背后的普遍規律，而不是單純地記憶數據樣本，從而提升模型的泛化性能。正則化方法種類繁多，其通過改造損失函數或優化器、對抗訓練、擴充數據集、集成模型等手段，使模型訓練過程更加穩健，避免模型對訓練數據的過擬合。

本研究介紹一種低成本、高通用性的正則化方法Sharpness Aware Minimization（SAM），從優化器的角度提升模型的泛化性能。該方法對傳統優化器梯度下降的算法進行改進，提出了魯棒性更強的SAM優化器，通過尋找權重空間內的“平坦極小值”，使模型不僅在訓練集上表現良好，且在樣本外同樣表現穩定。SAM優化器提出后，學術界陸續迭代出了各類改進的SAM優化器，從不同角度進一步增強SAM優化器的表現。

本研究在GRU模型的基礎上應用SAM優化器及其各類改進版本進行實驗，結果表明：

SAM優化器相較于傳統優化器在模型訓練過程中驗證集上過擬合速度降低，且損失函數曲面平坦度提升，展現出更強的泛化性能；
SAM優化器及其改進版本訓練模型預測因子2016-12-30至2024-09-30內多頭組年化收益31.4%，相較于等權基準信息比率4.0，相比基線模型提升顯著；
應用SAM優化器及其改進版本訓練模型構建指數增強組合，相較于GRU基線模型提升顯著，滬深300、中證500、中證1000指數增強組合超額收益提升在1-2 pct；
對比各SAM優化器訓練模型表現，回測全區間內GSAM模型預測因子指標及指增組合業績指標表現較好，ASAM模型2024年以來表現突出。

02SAM優化器與模型泛化性能

正則化方法

正則化方法（regularization）旨在使模型變得“更簡單”，防止過擬合。機器學習中的一個關鍵挑戰是讓模型能夠準確預測未見過的數據，而不僅僅是在熟悉的訓練數據上表現良好，即降低模型的泛化誤差。正則化的目標是鼓勵模型學習數據中的廣泛模式，而不僅僅記住數據本身。正則化方法通過各類手段，使訓練后的模型處于最佳狀態，在訓練數據和測試數據上取得同樣良好的表現。

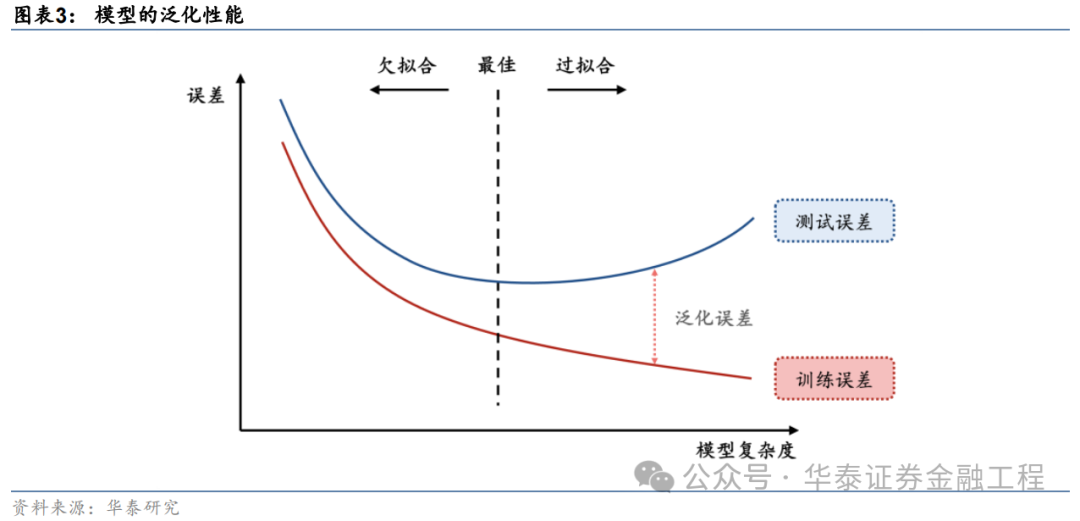
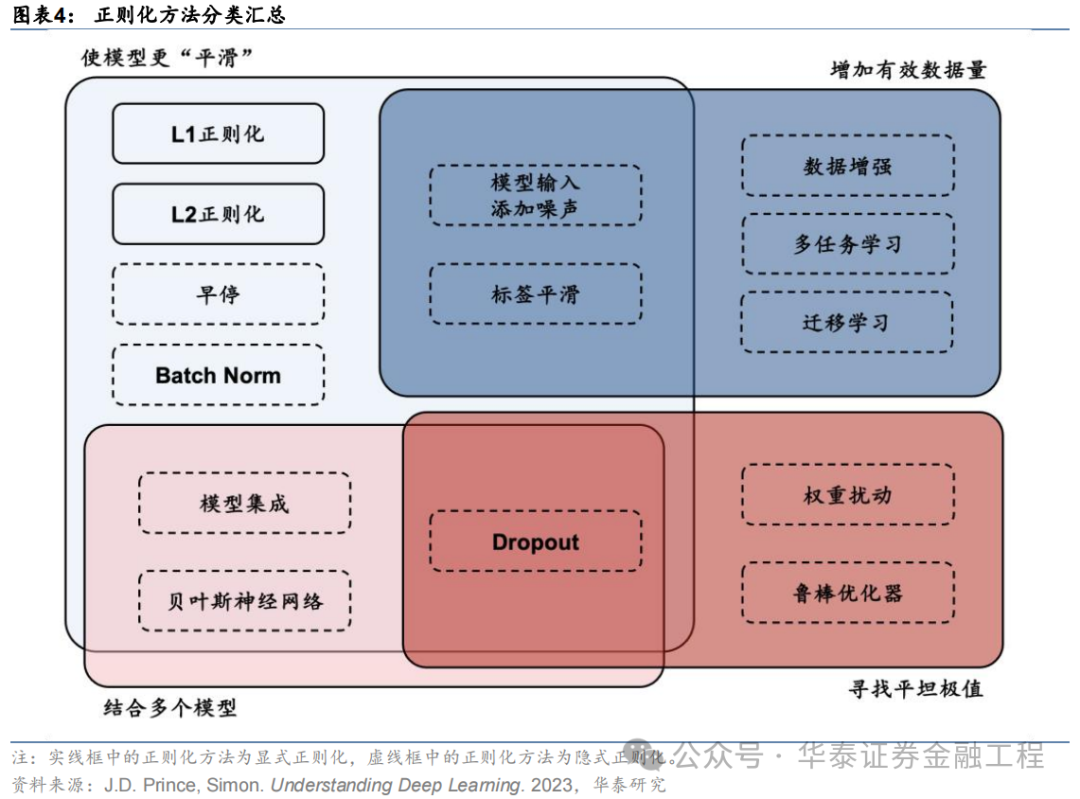
正則化方法的形式多樣。其中狹義的正則化通常指顯式正則化方法，即在損失函數中顯式添加一個懲罰項或約束，降低模型的復雜性，典型的顯式正則化項包括L1、L2正則化；而廣義的正則化通常指隱式正則化，其含義較為廣泛，在現代機器學習方法中無處不在，包括早停、Dropout、數據增強、去極值、多任務學習、模型集成等，幾乎所有致力于增強模型泛化性能的方法都可歸于此類。

傳統優化器及其局限性

深度學習領域中，優化器的選擇對于模型訓練的效率和最終性能至關重要。在眾多優化算法中，隨機梯度下降（SGD）及其變體是最為基礎且廣泛使用的優化方法之一。SGD通過逐次或批量更新權重來最小化損失函數，盡管簡單有效，但其學習率的選擇和振蕩問題是主要局限。為了克服這些問題，Adagrad、RMSprop以及Adam等優化器被陸續提出，有效提升了SGD優化器適用性和性能。下表匯總了深度學習中常用的傳統優化器的特點和局限性。

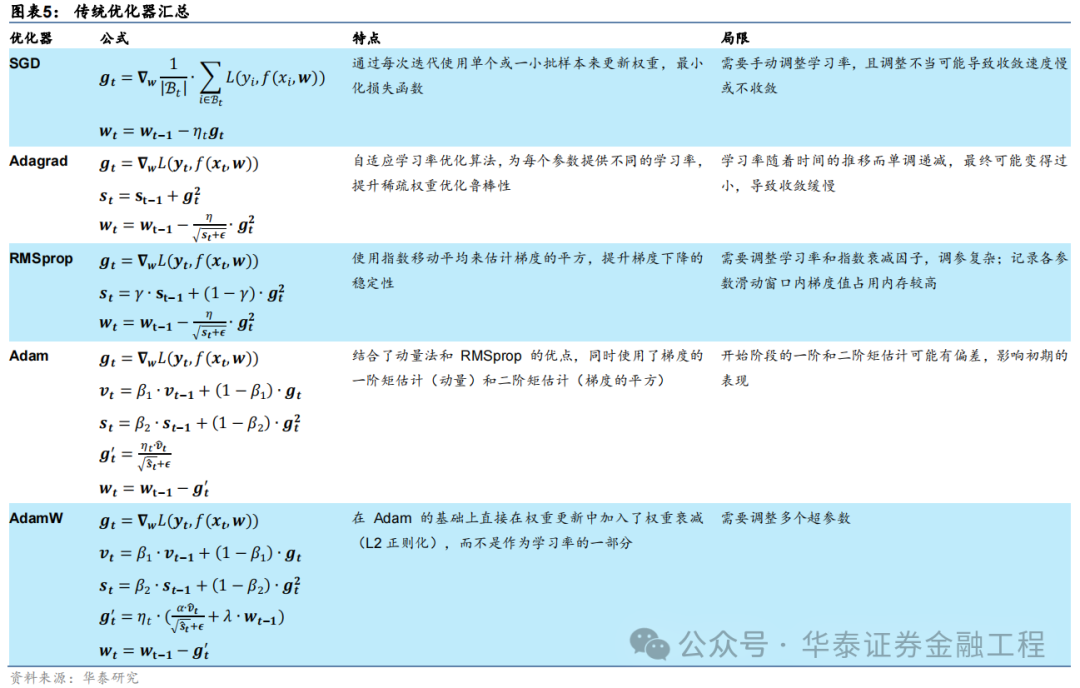
除了以上匯總的優缺點，傳統的優化器相比本文介紹的SAM優化器還有一個共同的局限：傳統優化器通常只考慮最小化訓練集上的損失函數，可能陷入“尖銳極小值”，這些極小值點處雖然訓練損失較低，但往往會導致過擬合現象，即模型對訓練數據過度擬合而泛化性能較差。相比之下，SAM優化算法能夠克服這些局限性，在訓練時尋找“平坦極小值”，這些極小值不僅在訓練集上表現出較低的損失，而且在測試集上也具有較好的泛化性能。

Sharpness?Aware?Minimization

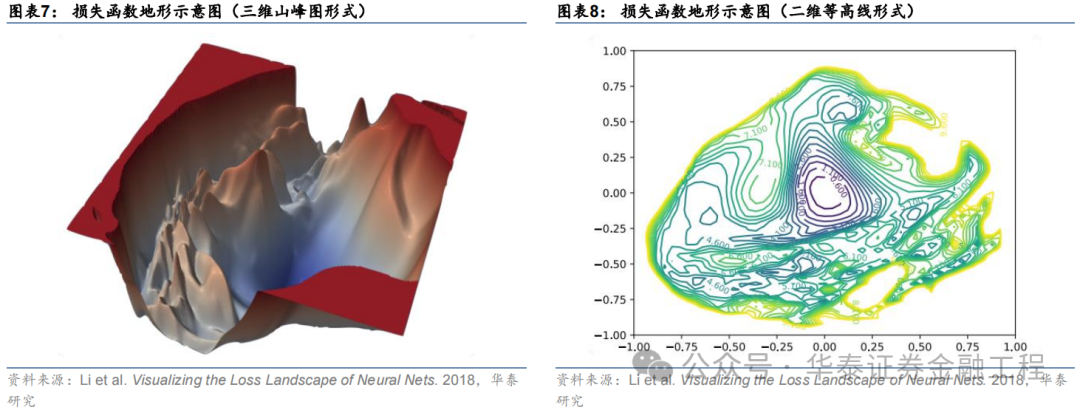
Sharpness Aware Minimization（SAM）方法最初由Google Research團隊Foret等人（2021）提出。該方法的出發點為對模型進行優化時，不僅希望優化后的模型權重所處位置損失函數較小，同時還希望該位置在模型權重空間中損失函數的“地形”較為平坦。由此引申出三個問題：什么是損失函數“地形”？為什么平坦的極值點處模型的泛化性能較優？如何追求平坦的極值點？

什么是損失函數“地形”？

損失函數地形即損失函數值與模型參數之間的變化關系。在優化問題中，損失函數可看作以模型參數為自變量的函數，用公式表示即

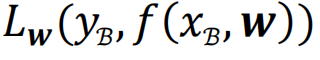
。對于神經網絡這類具有大量參數的模型，自變量為一個高維向量。若不對模型參數進行降維處理，則損失函數地形為高維空間中的一個曲面，曲面上的每一個點代表一組自變量取值時的損失函數值。

由于高維空間損失函數曲面難以可視化，作為研究對象不夠直觀，因此通常可對模型參數降維，通過簡化后的低維空間進行可視化和理解。舉例來說，假設模型中只有一個可變參數，則此時損失函數地形即退化為一維的損失函數曲線；同樣假設從高維模型參數中提取兩個主要分量作為模型參數，即可將損失函數與參數之間的變化關系用二維曲面進行表示，這也是最為常見的做法。

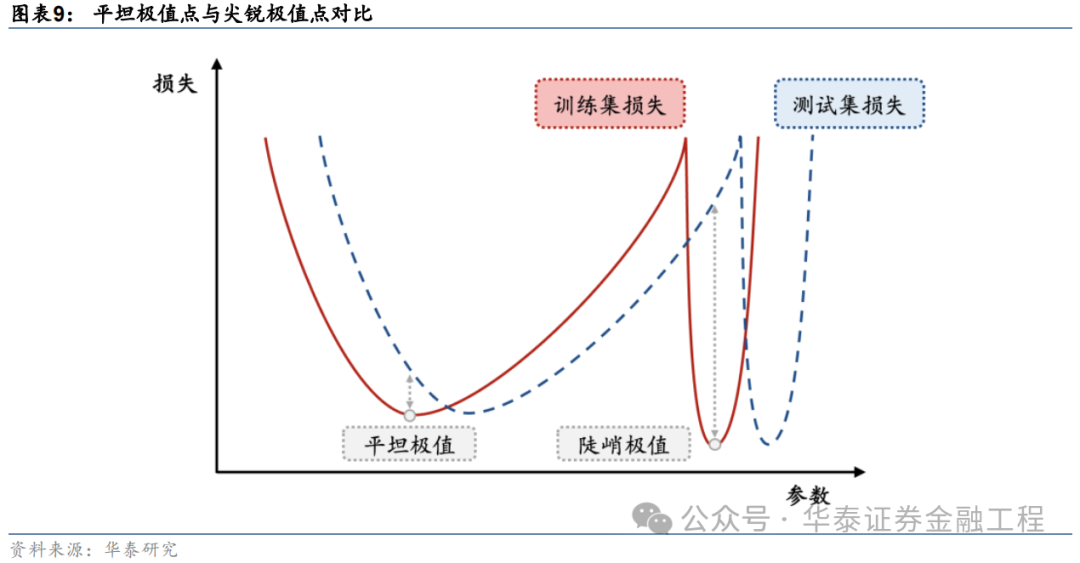
為什么平坦的極值點處模型的泛化性能較優？

以一維損失函數曲線為例進行說明。下圖展示了兩個形態不同的極值點，其中左邊的極值點較為“平坦”，即損失函數隨著模型參數的變化較小，而右邊“尖銳”的極值點則相反。若模型訓練完成后處于右邊的“尖銳”極值點，雖然其在訓練數據上的損失函數值較小，但當模型在測試數據上進行實際預測時，由于測試數據與訓練數據之間分布的偏差，預測結果將會產生較大誤差。而若模型訓練完成后處于左邊的“平坦”極值點，則測試數據與訓練數據的偏差給模型預測帶來的影響就相對微小。

如何追求平坦的極值點？

SAM優化器通過兩次梯度下降，微調梯度下降的方向來尋找權重空間中較為平坦的極值點。具體做法為：將傳統的優化器的優化目標從優化一個權重點位置處的損失函數改為優化這個點以及其擾動范圍內全部點損失函數的最大值。用公式表達即：

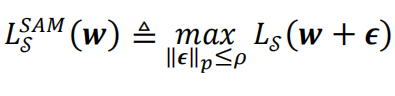
其中代表優化的目標函數，代表模型權重，而則代表權重點附近的一個微小擾動值，為控制該擾動值大小的超參數。

而某權重點擾動范圍內損失函數最大值的位置其實是已知的。常規優化算法梯度下降時沿著該權重點處損失函數的負梯度方向前進，可使損失函數最速下降。因此，損失函數最大值的位置的方向即損失函數的正梯度方向。在該權重點處沿著損失函數正梯度方向前進一小步的位置即擾動范圍內損失函數最大值處。用公式表達即：

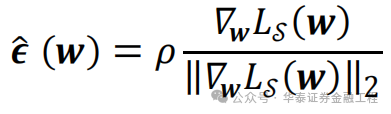
其中，

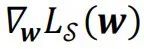
為損失函數在處的梯度，而分母中的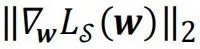

則表示該梯度張量的二階模。

表示的就是損失函數上升最快的擾動方向，

將

代入

中并求梯度，經過泰勒展開及近似，就可以得到SAM優化算法在訓練時每一步實際更新的梯度：

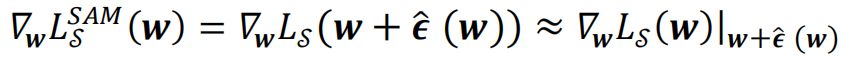
即在SAM算法中，

每一次梯度下降時用損失函數在

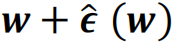
處的梯度更新點處的模型權重

SAM優化器算法流程示意圖和偽代碼如下圖所示。

SAM優化器的改進

SAM優化器一經提出即在學術界引起了廣泛關注。SAM優化器通過簡潔有效的算法邏輯增強了模型的泛化性能，但同樣也存在多方面的改進空間。許多改進版本的SAM優化器被陸續提出，匯總如下：

對SAM優化器的改進主要分為兩個方向，分別著重優化SAM優化器的性能和效率。對于應用于量化選股的AI模型而言，優化器的泛化性能才是最終決定模型預測效果的因素，因此優化器的效率相較于其性能并不關鍵。接下來簡要介紹著眼于改進性能的幾種改進SAM優化器。

ASAM

Adaptive Sharpness Aware Minimization（ASAM）由Kwon等（2021）提出。ASAM優化器相較于SAM優化器的改進類似于Adagrad優化器相較于SGD優化器的改進，區別在于后者調整學習率大小以適應神經網絡中不同參數的尺度，而前者調整權重空間內擾動半徑以適應神經網絡中不同參數的尺度。ASAM優化器引入了自適應擾動半徑的概念，在計算權重空間內擾動半徑時考慮到各參數的尺度，因此通過該方法計算得到的SAM優化路徑與各參數本身的尺度無關，解決了SAM中銳度定義的敏感性問題，提高了模型的泛化性能。

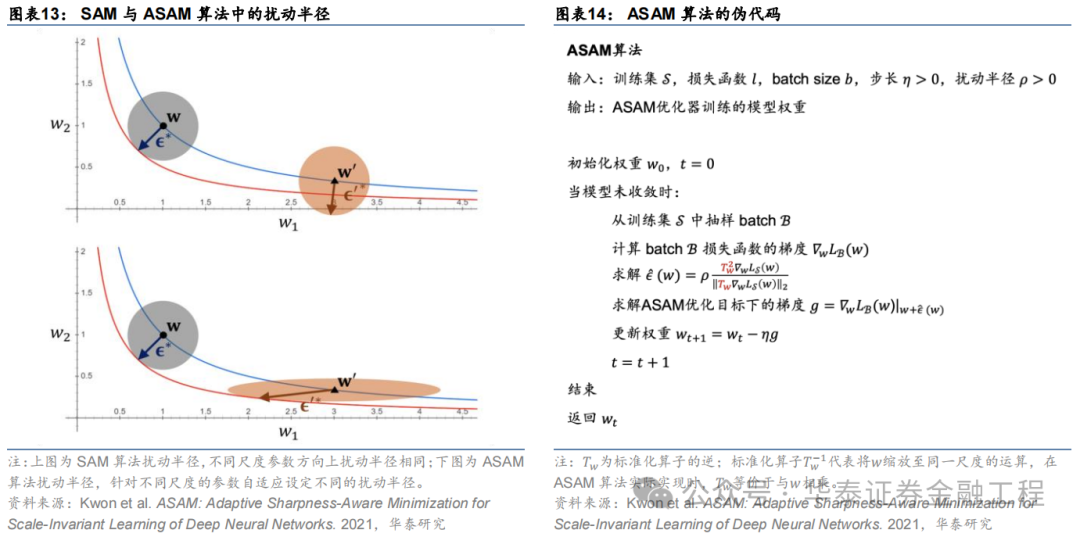
GSAM

Surrogate Gap Guided Sharpness Aware Minimization（GSAM）由Zhuang等（2022）提出。該研究發現擾動后損失與擾動前損失之差（即surrogate gap）更能準確衡量模型權重空間極小值處損失地形的平坦度。由此進一步推導出GSAM優化器的梯度更新方法：第一步類似于SAM，通過梯度下降最小化擾動損失；第二步則在實際更新權重時首先將擾動前梯度在擾動后梯度方向上投影得到垂直分量，接著將擾動后梯度與該垂直方向分量相加得到最終梯度下降的方向，更新模型權重。

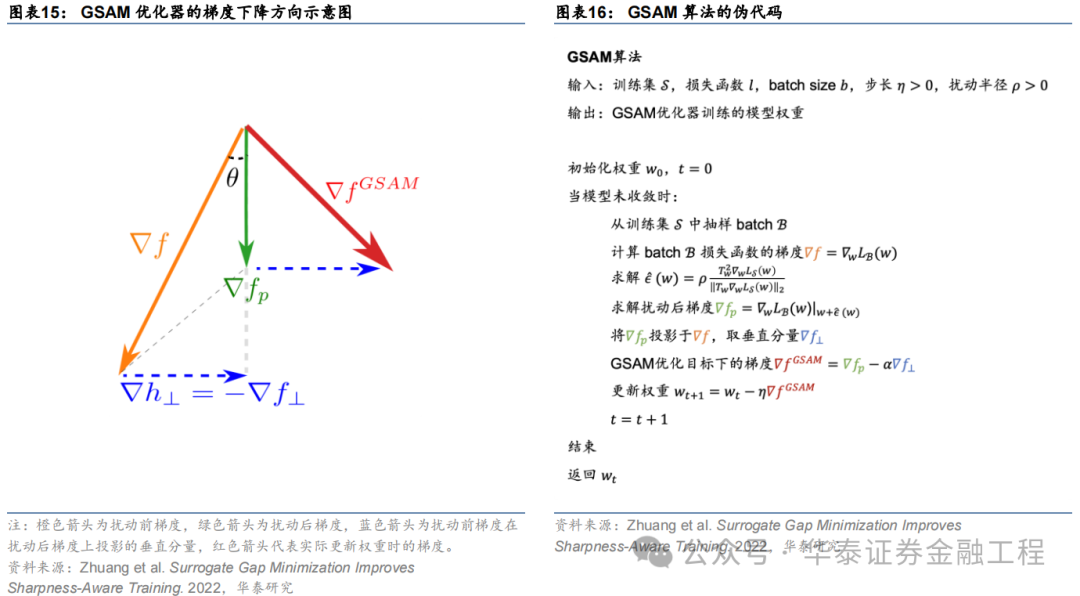
GAM

Gradient Norm Aware Minimization（GAM）由Zhang等（2023）提出。本研究發現，應用SAM方法時常常因為小區域內存在多個極值點的情形導致“誤判”：即使在小擾動半徑內損失函數波動非常劇烈，但因為擾動后參數點的損失函數與擾動前差距較小而認為在該擾動范圍內損失函數是“平坦”的。因此，GAM方法通過同時優化擾動半徑內的零階平坦度（損失函數平坦度）以及一階平坦度（梯度平坦度）避免了該種“誤判”。

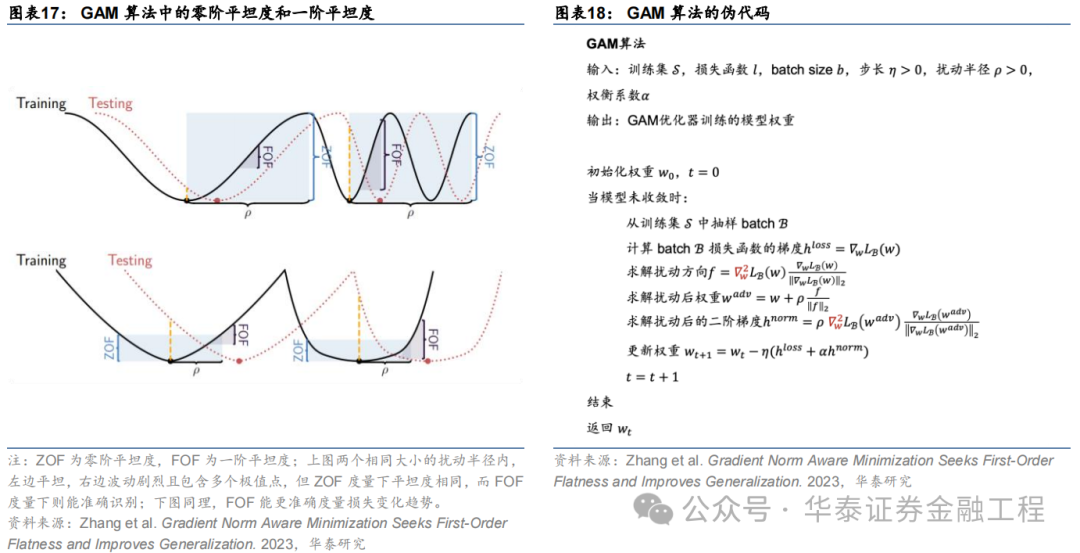
FSAM

Friendly Sharpness Aware Minimization（FSAM）由Li等（2024）提出。研究發現SAM優化器的擾動方向可以被分解為全梯度分量和僅與每個小批量相關的隨機梯度噪聲分量，且前者對泛化性能的有顯著的負面影響。FSAM優化器通過指數移動平均（EMA）估計擾動方向中的全梯度分量，并將其從擾動向量中剝離，僅利用隨機梯度噪聲分量作為擾動向量，成功減少了全梯度成分對泛化性能的負面影響，從而提高了模型的泛化性能。

03實驗方法

基線模型

本研究基于端到端的GRU量價因子挖掘模型測試SAM優化器的改進效果。基線模型的構建方法如下圖，分別使用兩個GRU模型從日K線和周K線中提取特征得到預測值，作為單因子，再將兩個單因子等權合成得到最終的預測信號。GRU模型的構建細節可參考《神經網絡多頻率因子挖掘模型》（2023-05-11），本文不做展開。

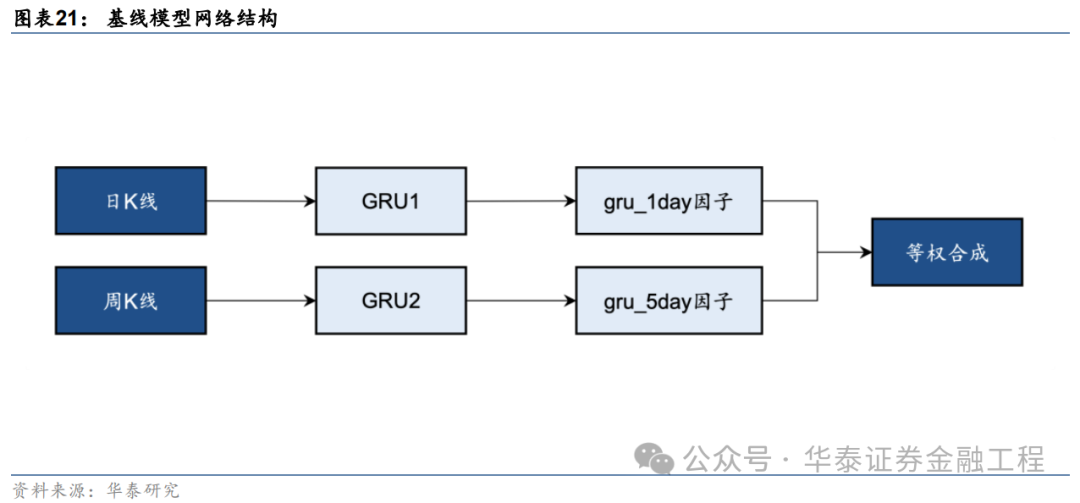
基線模型輸入數據細節及訓練超參數設置如下表：

SAM優化器

SAM優化器的突出特點即適用性強，同一種SAM優化器能夠封裝各類不同的基礎優化器，而無需對模型訓練的流程進行大范圍的修改。本研究將SAM優化器應用于基線模型，GRU的網絡結構及超參數均不做改變，僅改變模型訓練時使用的優化器。其中，SAM優化器及其4種改進版本均選取AdamW作為基礎優化器，優化器的學習率、動量和權重衰減等超參數均不做調整。5組對比實驗采用的SAM優化器及其特有參數取值匯總如下。

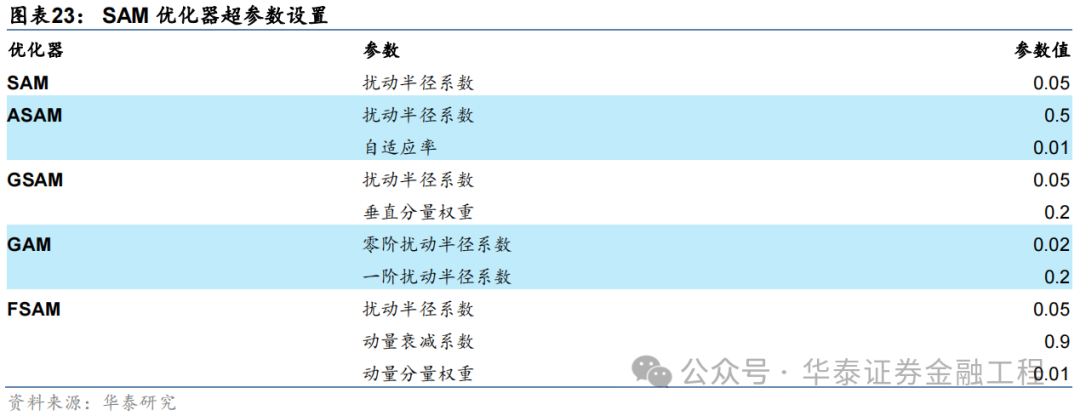
04?實驗結果

本研究在GRU基線模型的基礎上，保持模型結構、數據集不變，改變訓練使用的優化器共進行6組對比實驗。以下分別從模型訓練時的收斂性、損失函數地形、模型預測因子表現和基于模型構建指數增強組合業績等方面展示實驗結果。

模型收斂性

模型訓練過程中損失函數和評價指標在驗證集上表現的變化趨勢是模型泛化性能最直觀的體現。若訓練時隨著Epoch增加，驗證集的評價指標短暫提升后迅速下降，則說明模型過擬合嚴重，泛化性能不佳；反之，若驗證集的評價指標隨著Epoch增加穩健提升，則說明模型泛化性能較好。

本節選取相同種子點、相同數據集下的基線模型與SAM模型，對比訓練過程中兩者在驗證集上IC、IR等指標的變化趨勢。

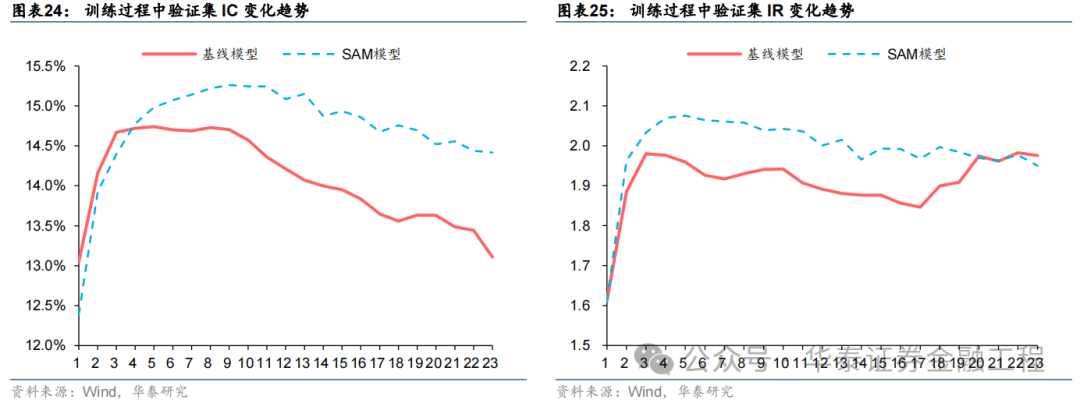
結果表明，基線模型與SAM模型在驗證集上IC、IR指標變化趨勢均為先上升后下降，但相較而言，SAM模型下降幅度較緩，且訓練過程中指標最大值均高于基線模型，證明SAM優化器有效抑制了過擬合，提升了模型的泛化性能。

損失函數地形

SAM優化器設計初衷是使模型訓練時在權重空間中找到一條平緩的路徑進行梯度下降，即每次權重更新時損失函數不劇烈變化，最終在權重空間中停留在一個平坦的極值點處。因此，本節嘗試對模型權重空間上的損失函數進行可視化，以檢驗SAM優化器的應用效果。

循環神經網絡的權重通常包含數以萬計的參數，以GRU為例，輸入時序維度為30、隱藏層維度為64、特征數為6、層數為2的網絡共包含40000多個權重參數，每次梯度下降時，優化器同時對所有參數迭代更新。因此，可視化一個數萬維度權重空間上的損失函數值并非易事。常見的解決方法為通過PCA、t-SNE等技術將高維空間的權重降維至二維或三維，從而繪制一幅損失函數“地形圖”。

本研究采用PCA方法，繪制損失函數“地形圖”，具體步驟如下：

選取訓練軌跡上驗證集最優權重作為原點；
對訓練軌跡上的所有權重向量運用主成分分析，從中提取出兩個主成分向量，分別作為二維圖像的兩個軸方向；
生成一組二維離散點陣作為圖像每個像素點的坐標，并對每個坐標點對應的神經網絡權重在給定數據集上使用全部樣本進行一次推理，計算損失函數值，作為該點的像素值。該步驟完成后即可繪制出一張二維的損失函數地形圖像；
將模型訓練時每個Epoch的模型權重投影至該二維平面，實現模型訓練軌跡的可視化。

依據該方法，本文選取基線模型與SAM模型，在相同數據集和相同的隨機數種子點的前提下，分別繪制損失函數地形圖。繪制時對兩組實驗分別選取主成分軸，并采用相同的損失函數等高線和相同的像素分辨率，分別繪制訓練集和測試集上的損失函數地形，結果如下：

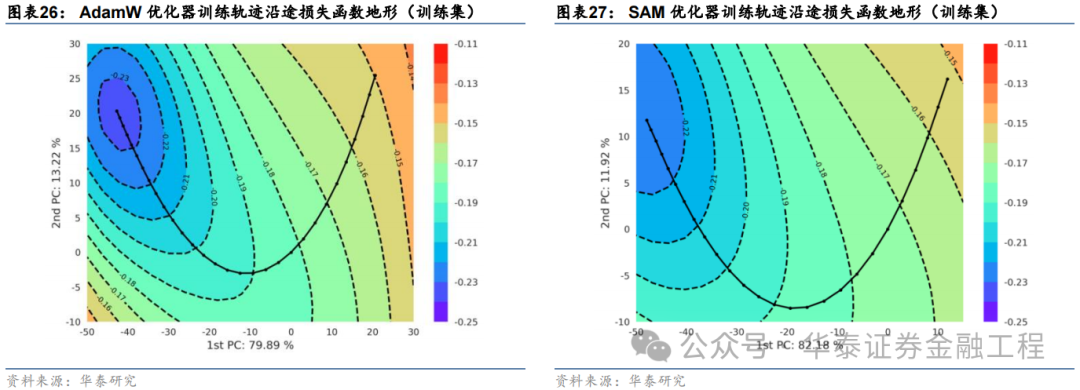
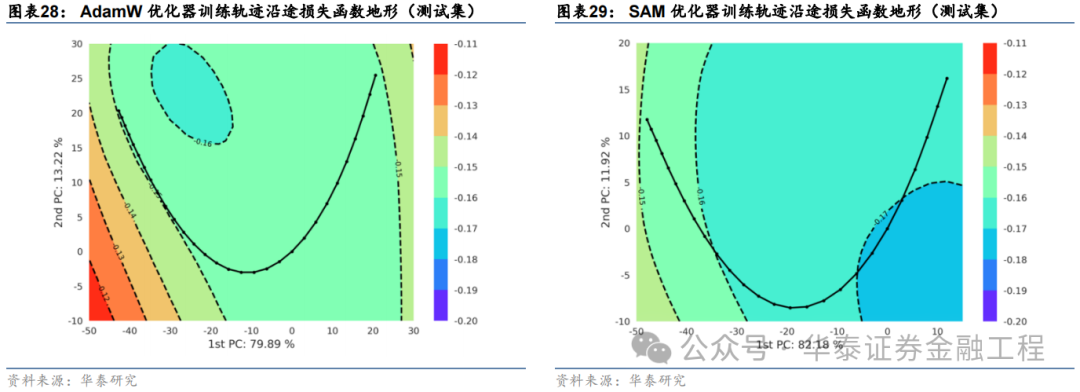
對比以上結果發現：

兩組實驗的第一主成分軸均達到80%左右的方差貢獻率，且兩個主成分軸的累計貢獻率均超過了90%，說明兩幅損失函數曲面圖均能很好的反映訓練軌跡沿途損失函數的變化趨勢；
訓練集上基線模型損失函數地形圖等高線較為密集，而SAM模型損失函數地形圖等高線較為稀疏且分布均勻，說明SAM優化器能有效改善損失地形的平坦度，符合預期；
SAM模型在測試集上的損失函數地形與基線模型相比整體損失函數值較低，其中SAM模型早停處損失函數值小于-0.17，而基線模型早停處損失函數值大于-0.16，說明SAM模型泛化誤差較小，即在訓練數據與測試數據上表現同樣良好，有效抑制了過擬合。

因子表現

針對6組實驗，分別測試模型預測因子表現。單因子測試的細節如下：

測試結果如下，可得出如下結論：

SAM模型與基線模型預測因子RankIC及RankICIR表現接近，表明將傳統優化器改為SAM優化器并未顯著提升模型預測因子的RankIC表現；
5組SAM模型TOP組收益率均高于基線模型，其中GAM、GSAM、FSAM組提升較為明顯，FSAM模型表現最佳。證明應用SAM優化器能有效改善預測因子多頭端預測準確性，提升多頭組表現；
幾組實驗預測因子分層效果均較為優異，多頭端收益5組SAM優化器模型普遍高于基線模型。

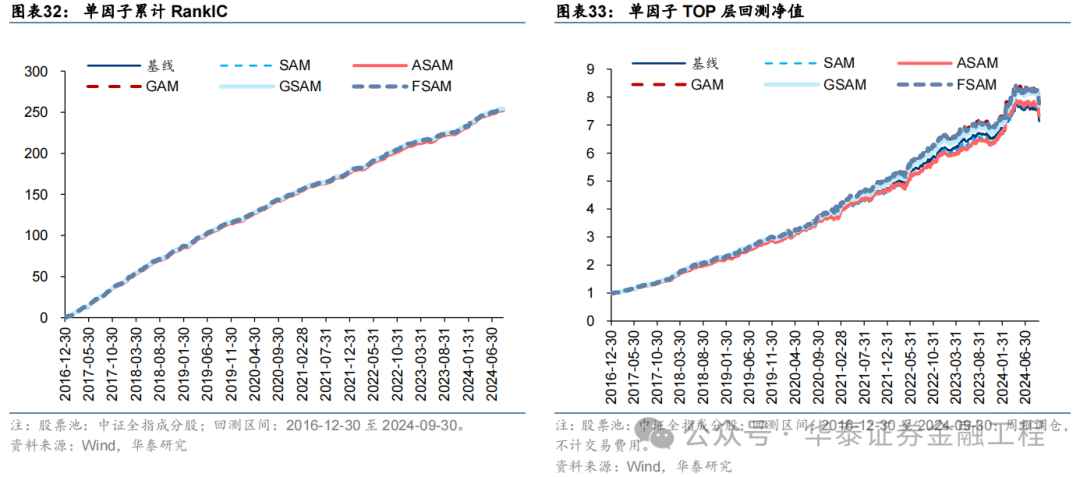
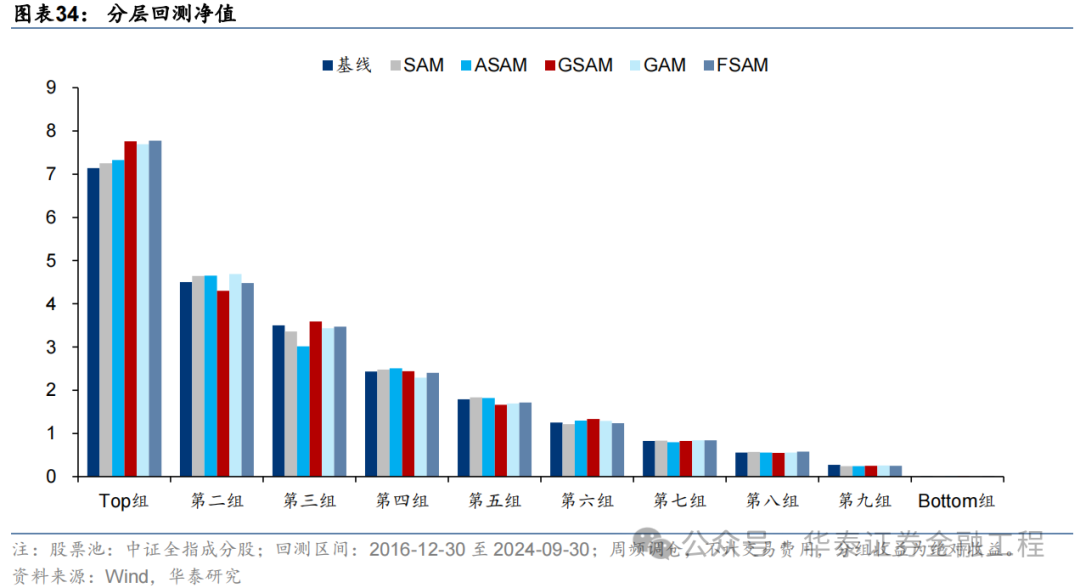
指數增強組合表現

將以上6組實驗得到的預測因子應用于組合優化，分別構建滬深300、中證500及中證1000指數增強組合。組合優化及回測細節如下。

滬深300增強組合

基于6組實驗預測因子構建的滬深300指數增強組合回測結果如下。測試結果表明，SAM模型及4個改進模型年化超額收益及信息比率相較于基線模型均有穩定提升。其中GSAM模型表現最佳，年化超額收益、信息比率、超額收益Calmar比率及勝率在幾組實驗中均排名第一。

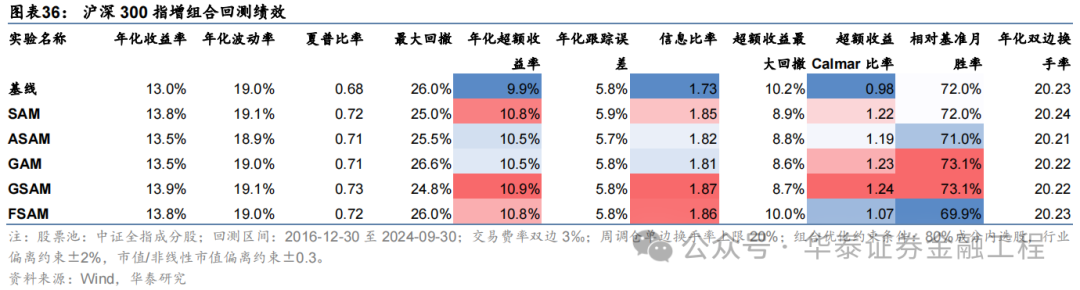
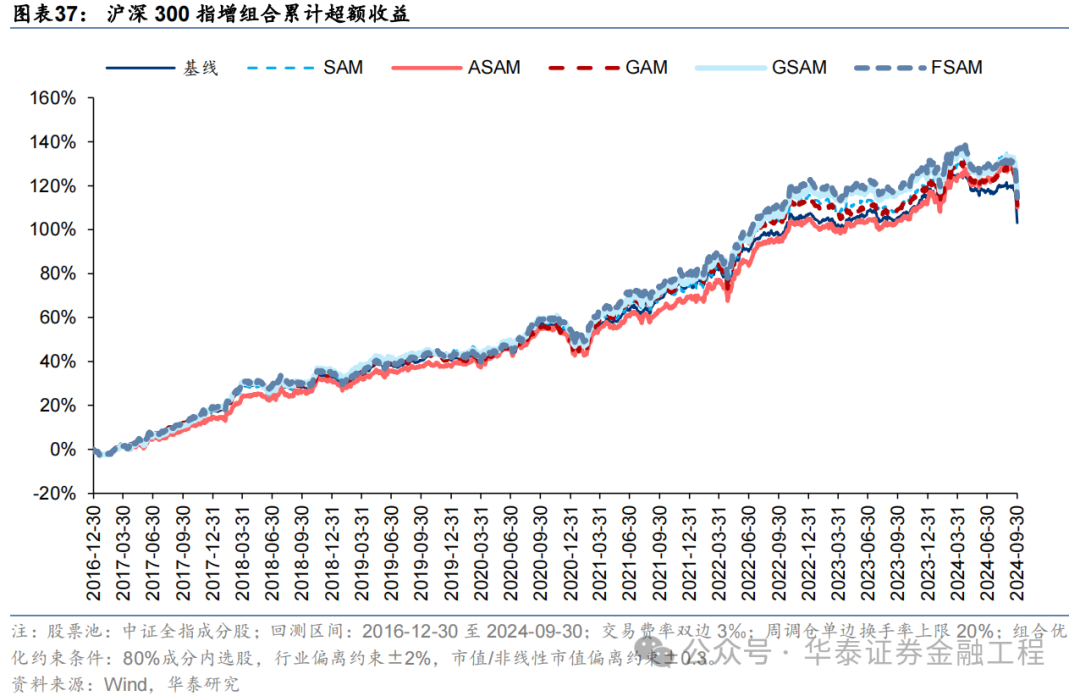
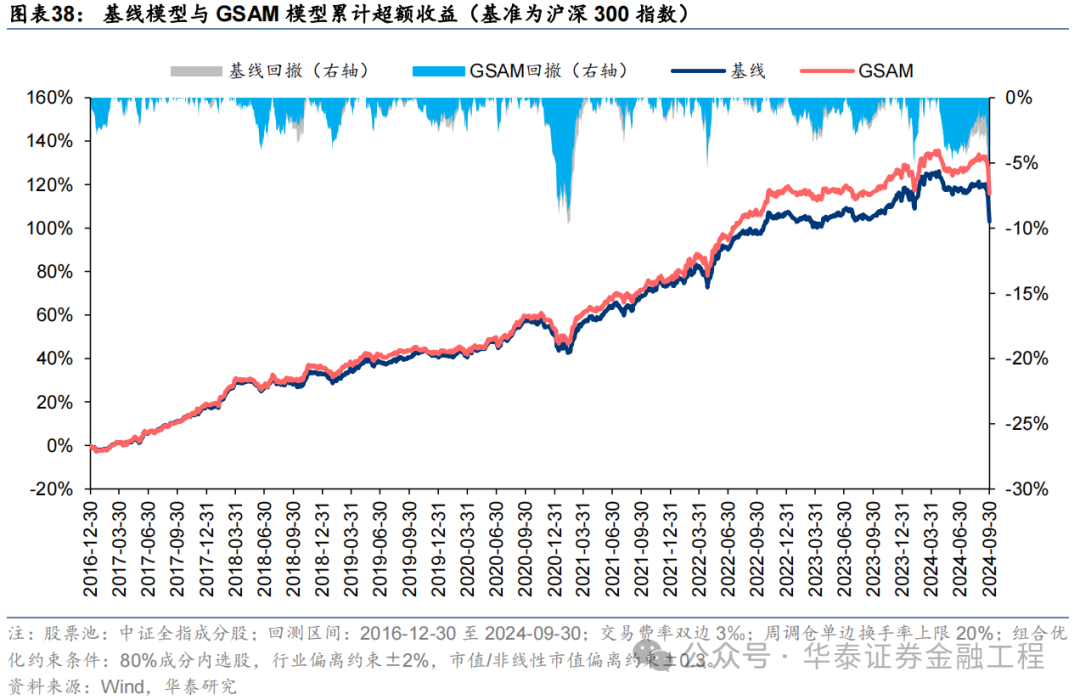
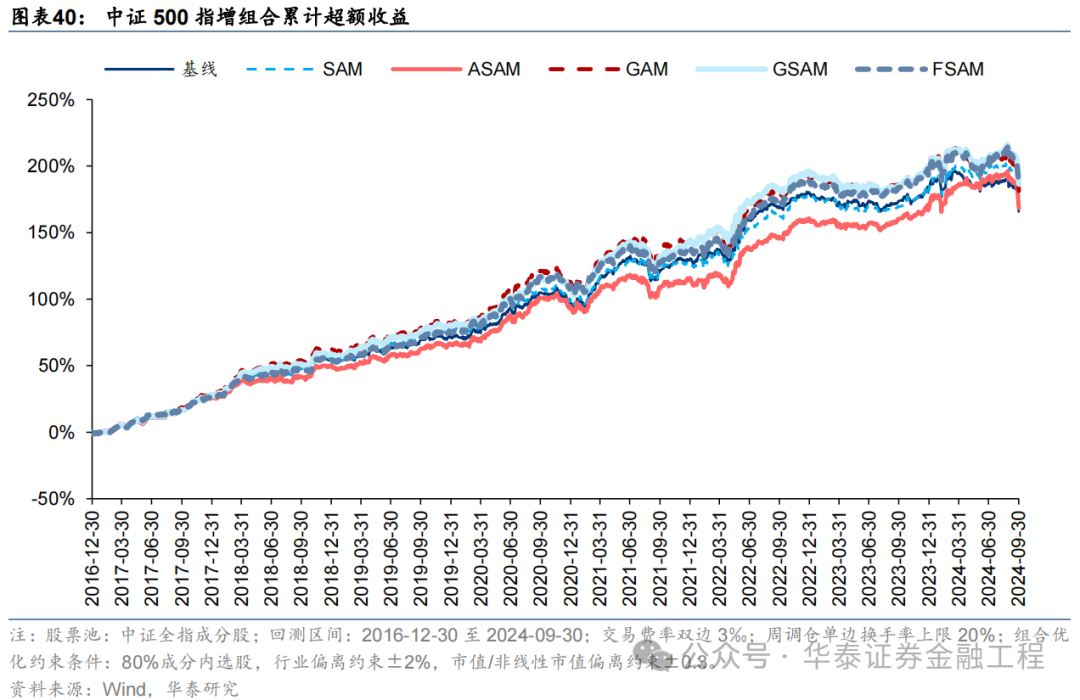
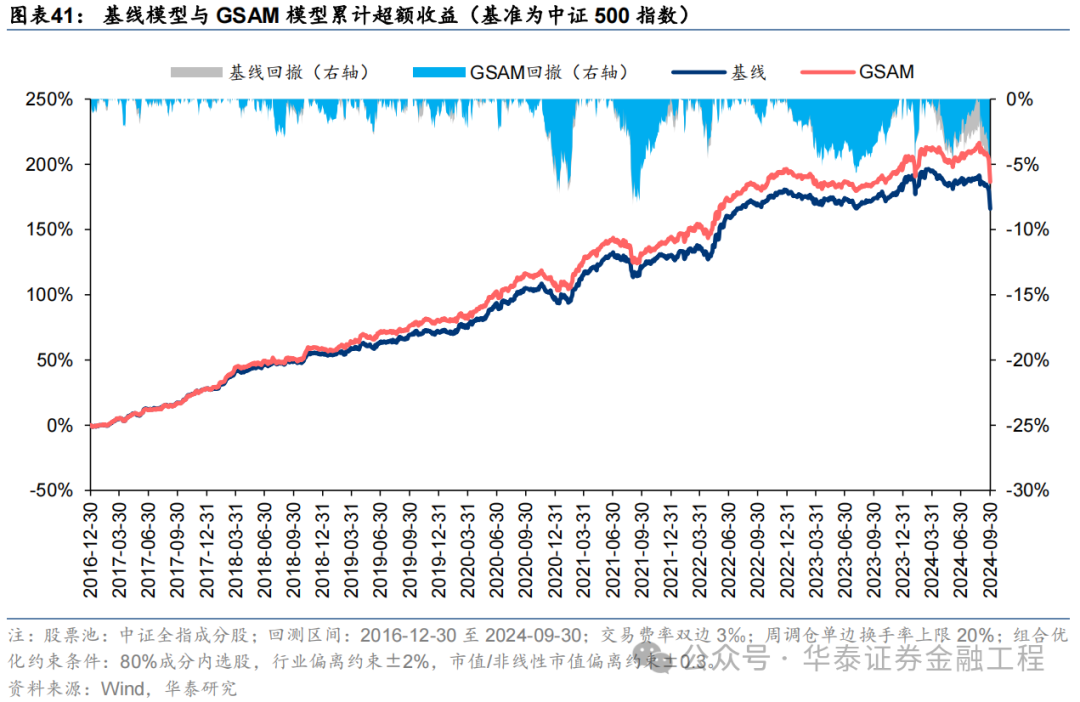
中證500增強組合

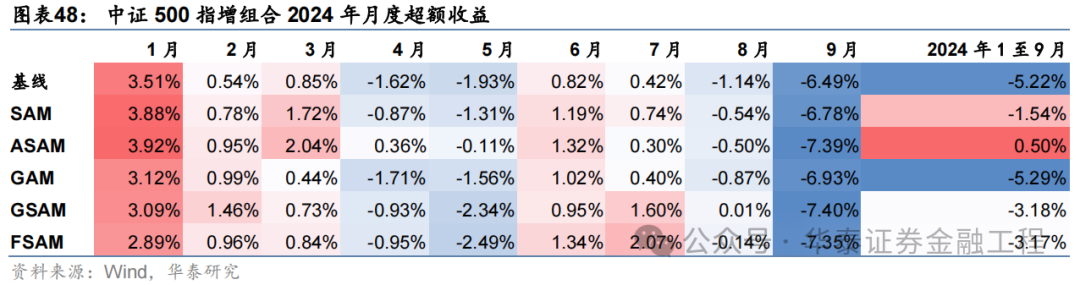
基于6組實驗預測因子構建的中證500指數增強組合回測結果如下。測試結論與滬深300類似，GSAM模型年化超額最高為15.1%，FSAM模型信息比率最高為2.29。另外，除了GAM模型外，其余模型在回撤控制和月度勝率方面相較于基線模型也同樣具有優勢。

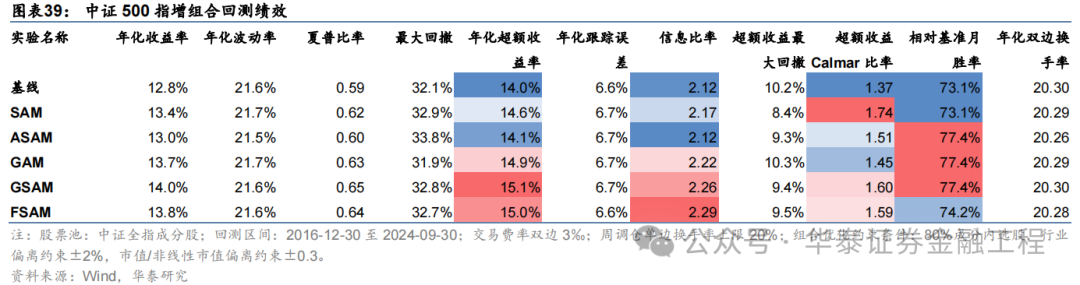
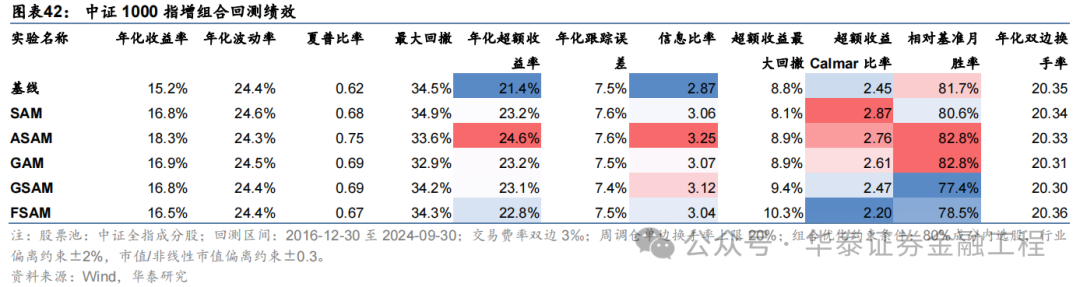
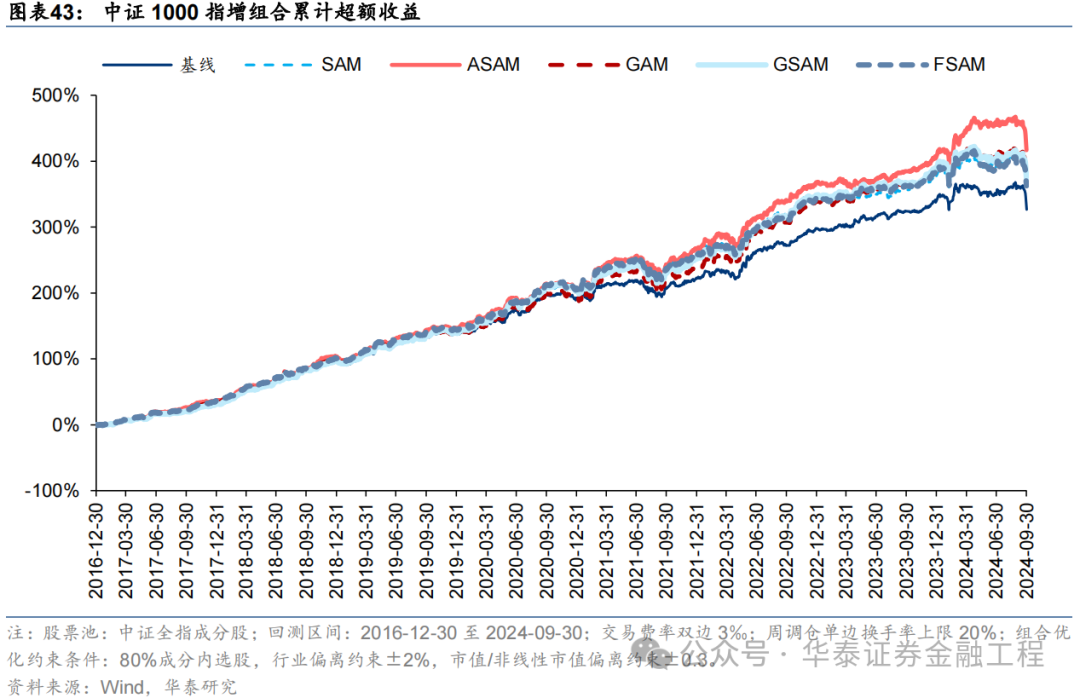
中證1000增強組合

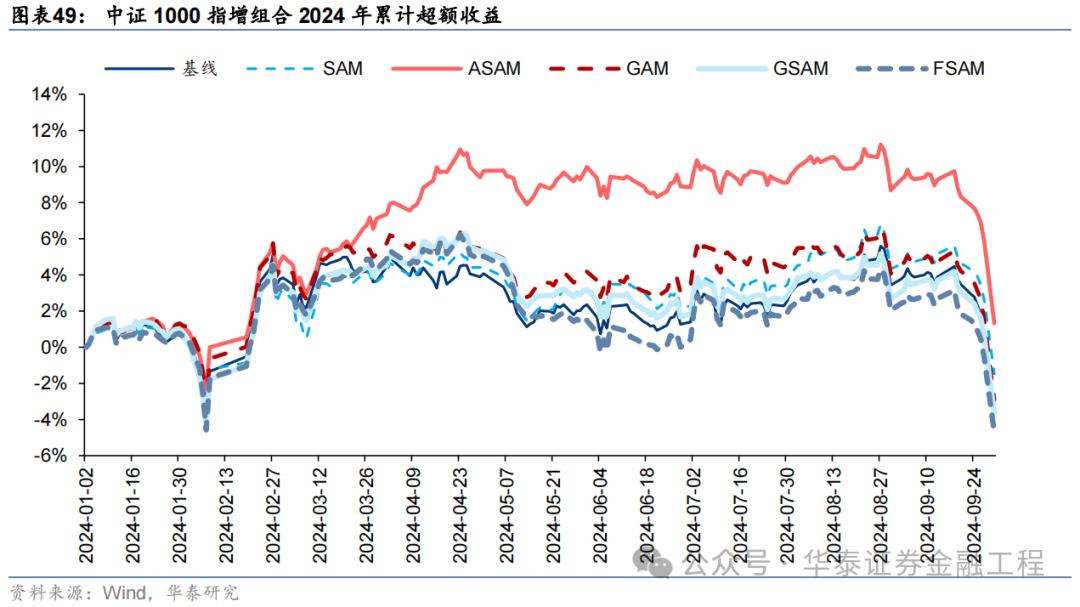
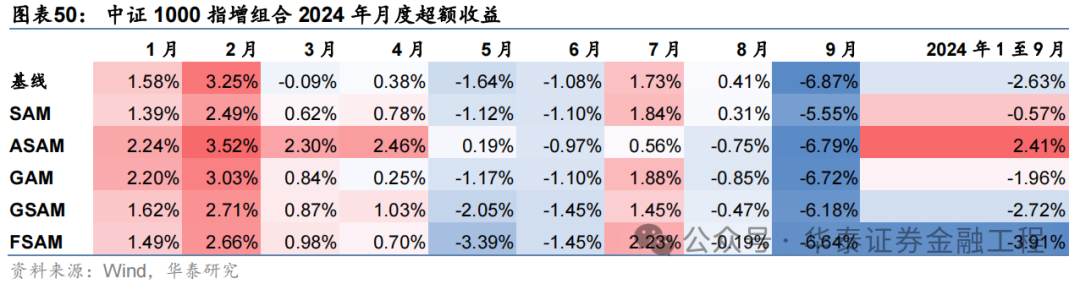
基于6組實驗預測因子構建的中證1000指數增強組合回測結果如下。測試結果表明，SAM優化器模型在年化超額收益和信息比率指標上相對基線模型均有明顯優勢，可將年化超額收益提升2%，信息比率提升0.2左右。其中從超額收益及信息比率角度看表現最好的模型為ASAM，可將年化超額收益從21.4%提升至24.6%，信息比率從2.87提升至3.25。

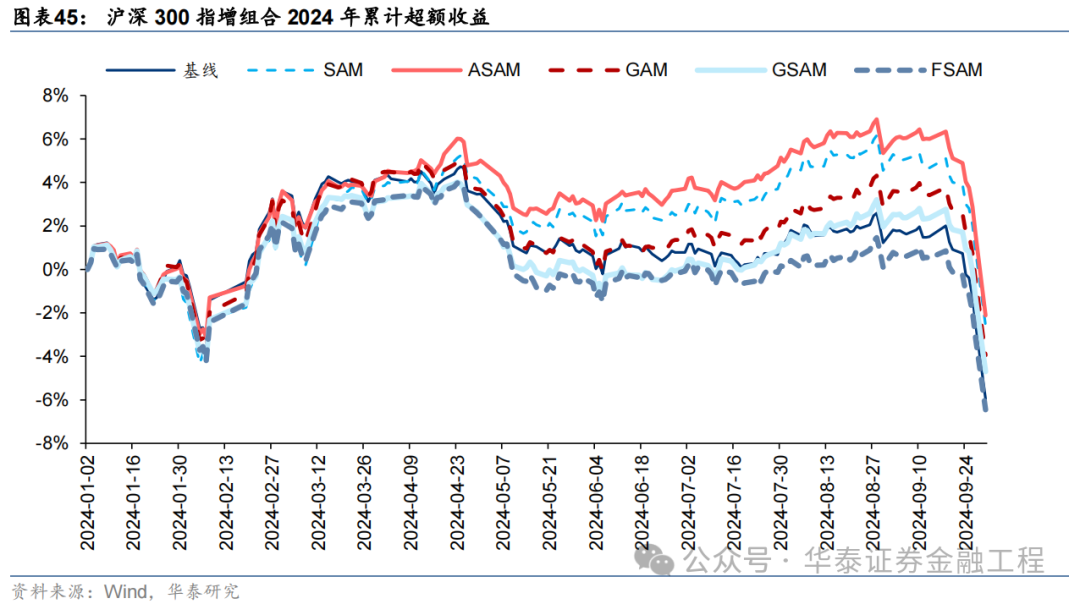
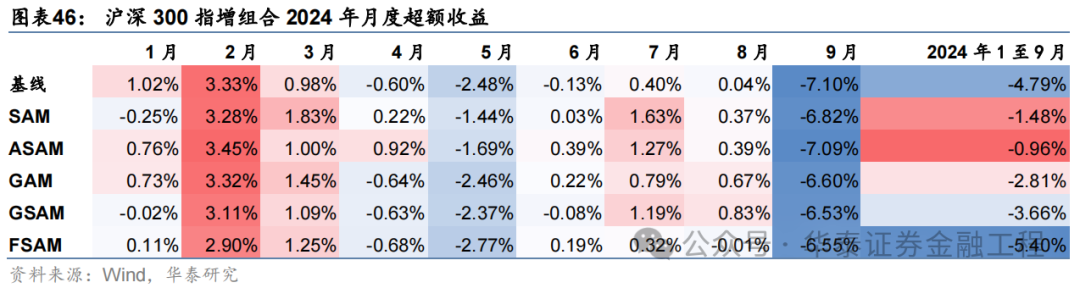
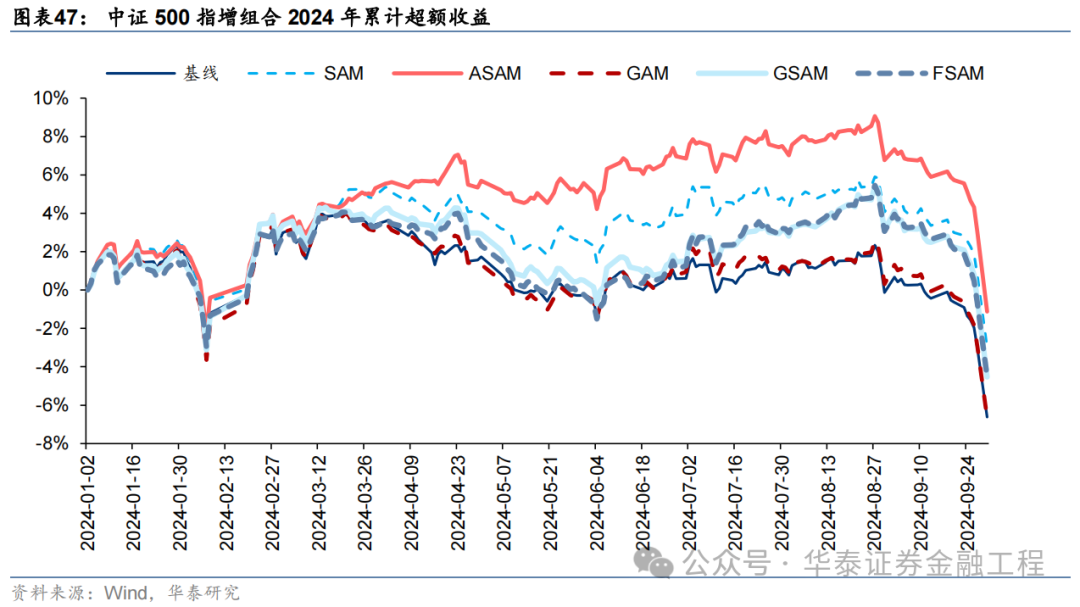
2024年業績表現

統計各指增組合2024年以來業績表現如下。分析發現，各指增組合在2024年9月末的大幅波動下超額收益均迎來顯著回撤。但SAM模型及其改進模型相對基線模型均具有穩定優勢。其中ASAM模型在2024年表現突出，三組指增業績均排名第一，且超額收益領先基線模型約5%。

05 總結

本研究介紹一種低成本、高通用性的正則化方法Sharpness Aware Minimization（SAM），從優化器的角度提升模型的泛化性能。本文首先綜述各類正則化方法在改善模型泛化性能中的重要性，其次分析SAM優化器相較于傳統優化器的改進及其原理，接著介紹學術界對SAM優化器的進一步改進，最后以端到端的GRU量價因子挖掘模型作為基線模型，改變訓練模型使用的優化器進行實證。結果表明應用SAM優化器能有效抑制模型過擬合，顯著提升模型預測因子的多頭端收益，且基于各SAM模型構建的指數增強組合業績均顯著優于基線模型。

SAM優化器通過追求“平坦極小值”，增強模型魯棒性。SGD、Adam等傳統優化器進行梯度下降時僅以最小化損失函數值為目標，易落入“尖銳極小值”，導致模型其對輸入數據分布敏感度高，泛化性能較差。SAM優化器將損失函數的平坦度加入優化目標，不僅最小化損失函數值，同時最小化模型權重點附近損失函數的變化幅度，使優化后模型權重處于一個平坦的極小值處，增加了模型的魯棒性。基于SAM優化器，ASAM、GSAM等改進算法被陸續提出，從參數尺度自適應性、擾動方向的準確性等方面進一步增強了SAM優化器的性能。

SAM優化器能降低訓練過程中的過擬合，提升模型的泛化性能。SAM優化器設計初衷是使模型訓練時在權重空間中找到一條平緩的路徑進行梯度下降，改善模型權重空間的平坦度。可通過觀察模型訓練過程中評價指標的變化趨勢以及損失函數地形圖對其進行驗證。從評價指標的變化趨勢分析，SAM模型在驗證集上IC、IR指標下降幅度較緩，訓練過程中評價指標最大值均高于基線模型；從損失函數地形分析，SAM模型在訓練集上損失函數地形相較基線模型更加平坦，測試集上損失函數值整體更低。綜合兩者，SAM優化器能有效抑制訓練過程中的過擬合，提升模型的泛化性能。

SAM優化器能顯著提升AI量化模型表現。本研究基于GRU模型，對比AdamW優化器與各類SAM優化器模型表現。從預測因子表現看，SAM優化器能提升因子多頭收益；從指數增強組合業績看，SAM模型及其改進版本模型在三組指數增強組合業績均顯著優于基線模型。2016-12-30至2024-09-30內，綜合表現最佳模型為GSAM模型，單因子回測TOP層年化超額收益高于31%，滬深300、中證500和中證1000增強組合年化超額收益分別為10.9%、15.1%和23.1%，信息比率分別為1.87、2.26和3.12，顯著優于基線模型。2024年以來ASAM模型表現突出，三組指數增強組合超額收益均領先基線模型約5%。

本研究仍存在以下未盡之處：

本研究測試SAM模型均采用文獻中推薦參數，并未針對AI量化模型做大范圍參數調優；
本研究僅對SAM優化器的性能改進版本優化器進行測試，未對效率改進版本的優化器進行測試。SAM優化器在訓練時需要進行兩次梯度下降，由此會帶來一定的額外計算成本，對SAM優化器的效率進行改進有望提升AI量化模型的訓練效率；
本研究對各改進版本的SAM優化器進行單獨測試，后續研究中可嘗試結合各類改進方向，得到一個綜合改進版本的SAM優化器。

參考文獻

Kwon, J., Kim, J., Park, H., Choi, I.K., 2021. ASAM: Adaptive Sharpness-Aware Minimization for Scale-Invariant Learning of Deep Neural Networks, in: Proceedings of the 38th International Conference on Machine Learning. Presented at the International Conference on Machine Learning, PMLR, pp. 5905–5914.

Sun, Y., Shen, L., Chen, S., Ding, L., Tao, D., 2023. Dynamic Regularized Sharpness Aware Minimization in Federated Learning: Approaching Global Consistency and Smooth Landscape, in: Proceedings of the 40th International Conference on Machine Learning. Presented at the International Conference on Machine Learning, PMLR, pp. 32991–33013.

Li, T., Yan, W., Lei, Z., Wu, Y., Fang, K., Yang, M., Huang, X., 2022. Efficient Generalization Improvement Guided by Random Weight Perturbation.

Du, J., Yan, H., Feng, J., Zhou, J.T., Zhen, L., Goh, R.S.M., Tan, V.Y.F., 2022. Efficient Sharpness-aware Minimization for Improved Training of Neural Networks.

Li, T., Zhou, P., He, Z., Cheng, X., Huang, X., 2024. Friendly Sharpness-Aware Minimization. Presented at the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 5631–5640.

Zhang, X., Xu, R., Yu, H., Zou, H., Cui, P., 2023. Gradient Norm Aware Minimization Seeks First-Order Flatness and Improves Generalization. Presented at the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 20247–20257.

Mi, P., Shen, L., Ren, T., Zhou, Y., Sun, X., Ji, R., Tao, D., 2022. Make Sharpness-Aware Minimization Stronger: A Sparsified Perturbation Approach.

Zhao, Y., Zhang, H., Hu, X., 2023. Randomized Sharpness-Aware Training for Boosting Computational Efficiency in Deep Learning.

Foret, P., Kleiner, A., Mobahi, H., Neyshabur, B., 2021. Sharpness-Aware Minimization for Efficiently Improving Generalization.

Du, J., Zhou, D., Feng, J., Tan, V., Zhou, J.T., 2022. Sharpness-Aware Training for Free. Advances in Neural Information Processing Systems 35, 23439–23451.

Zhuang, J., Gong, B., Yuan, L., Cui, Y., Adam, H., Dvornek, N., Tatikonda, S., Duncan, J., Liu, T., 2022. Surrogate Gap Minimization Improves Sharpness-Aware Training.

Liu, Y., Mai, S., Chen, X., Hsieh, C.-J., You, Y., 2022. Towards Efficient and Scalable Sharpness-Aware Minimization. Presented at the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 12360–12370.

Li, H., Xu, Z., Taylor, G., Studer, C., Goldstein, T., 2018. Visualizing the Loss Landscape of Neural Nets, in: Advances in Neural Information Processing Systems. Curran Associates, Inc.

風險提示：

人工智能挖掘市場規律是對歷史的總結，市場規律在未來可能失效。深度學習模型受隨機數影響較大。本文回測假定以vwap價格成交，未考慮其他影響交易因素。

（轉自：華泰證券金融工程）