來源：投資家

講一個大家可能耳熟能詳的故事吧。

在華盛頓州西雅圖附近出現了有史以來最偉大的一位電腦編程員。他意識到生產電腦芯片的英特爾是個朝陽企業，并且最早預測微型計算機必將大有市場。所以他決定為還未見起色的計算機編寫軟件。

20世紀70年代中葉，他自創公司，專門銷售微型計算機所需的軟件。公司成立伊始，“一切都顯得很荒唐離譜”，“公司的員工穿個褲衩，光著腳就來上班了”，“西裝革履的無一例外都是來訪者”。

但這個名不見經傳的小公司很快就財源滾滾。到了1981年，公司的操作系統在配備有英特爾微型處理器的個人電腦領域占據了絕對的市場份額。

公司初期取得了一系列成果，但接著卻面臨了一個分水嶺時刻。IBM于1980年夏前來拜訪，討論新一代個人電腦的操作系統合作。經過幾輪磋商，兩個公司達成一致協議。

1981年8月，電腦零售商在銷售新一代IBM個人電腦時附帶銷售這個新公司的軟件。公司的命運就此改變。之后的故事想必很多人都已知曉。

也許一些人對故事的后半部分不太熟悉，我還是再多說幾句吧。1994年7月8日，這位計算機技術的開拓者走進了位于加州蒙特利的一家飆車族酒吧。

他身穿摩托車皮夾克，可能他與人發生了爭斗，也可能無意中從高處跌落，總之這位開拓者頭部受到重創，扎掙著離開了酒吧，三天后死于傷勢加重和慢性酒精中毒，年僅52歲。他被安葬在西雅圖，墓碑上刻著軟盤的圖案。

他就是加里·基爾代爾。

你也許以為故事的主人公是微軟創始人－比爾·蓋茨。從故事的前半部分看，這樣想也不無道理。如果基爾代爾沒有英年早逝，他有沒有可能成為世界首富呢？

只是歷史是不能假設的。后來，IBM沒能與基爾代爾做成生意，蓋茨就自告奮勇攬下了這筆生意……

當人們問起微軟的成功在多大程度上靠的是運氣時，蓋茨說“運氣占相當大一部分”，“我們把握住好時機不完全靠運氣，但是沒有好運就沒有微軟的今天。”

我們的生活中，處處充滿運氣，我們對一個成功結果的評定，很難將實力和運氣區分開來。

這也是金融從業者邁克爾·莫布森所關心的方向，出生于1964年的莫布森畢業于喬治城大學，現任職于摩根史坦利投資管理公司，之前曾在瑞士信貸、藍山資本等工作過。除此以外，他還長期擔任哥倫比亞商學院的客座教授，以及復雜科學研究的發源地——圣塔菲研究所的董事會成員。

他于2012年出版《實力、運氣與成功》一書（The Success Equation），聚焦于實力與運氣在商業、體育及投資領域中的作用，并運用多學科思維模型對其深入分析探討。

對辨別一項活動需不需要實力，他提供了一個快速的方法：問一下自己失敗是不是因為自己不想贏。在靠實力取勝的活動中，自己不想贏就可以不贏；但玩輪盤賭或買彩票，再也不想贏也可能會贏。

而我們生活中常常試圖對于不能左右的“運氣”加以控制，而在自己能提高的“實力”上卻不加以努力。

美國神學家尼布爾的寫于1934年的經典安寧禱文曾說：

神啊，請賜予我內心安寧以接受我所不能改變的，請賜予我勇氣以改變我所能改變的，請賜予我智慧以分辨這二者之間的差別。

莫布森正是希望給讀者以智慧去分辨實力和運氣，以下選擇《實力、運氣與成功》第六章《運氣的表現形式：流行為什么成為流行？》，祝開卷有益！

在一些領域，運氣的鐘形分布曲線或者獨立事件就可以解釋很多現象。然而在娛樂世界里，成功和失敗都是社會相互作用的結果，根本無法預測結局。

對于一個事件，人們往往會評定很多等級，個人的觀念也很容易被他人的評價左右，一系列不確定因素讓成功來得太突然，失敗來得太令人費解。電影編劇威廉·高德曼不禁說了這樣一句俏皮話：“世人一無所知。”

舉個例子吧。假設一首歌比另一首歌在某段時間稍微流行些，在人們的相互影響下前一首歌就會越來越流行。本來兩首歌是同等水平、同樣的欣賞價值，最后卻一個唱遍大江南北，一個漸漸無人問津，這種現象就是“累積效應”。

“累積效應”讓人們幾乎沒法預測成功。實力當然對結果的好壞有影響，但是運氣的影響卻是壓倒性的。我們可以仔細探究下這種現象、背后的原理以及令人感到意外的結果。

社會的影響以及累積效應往往使得一個事件呈冪次定律分布。圖6-5顯示的是2010年美國最大的275個城市的排名和人口情況。橫軸是城市的排名，縱軸是城市的人口。圖中的城市分布大致在同一條斜線上，正好可以用冪次定律來表達。

通過冪次定律可以得出美國第17大城市得克薩斯州圣安東尼奧市的人口為132.5萬，美國第70大城市紐約的布法羅人口為26萬。

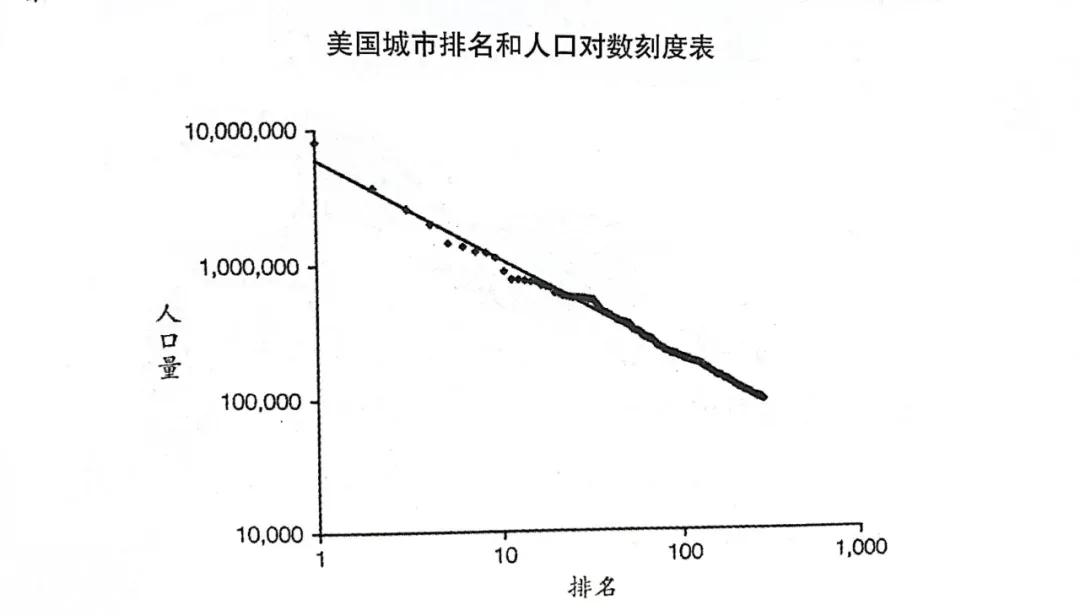圖6-5

冪次定律來自這樣一個事實，指數（或冪）決定斜率。很多社會現象都遵循冪次定律，比如說圖書銷售的排名和銷量、科技論文的排名和引用率、恐怖活動地區的排名和死亡人數，以及戰爭的規模和遇難人數等。

遵循冪次定律分布的事件具有的主要特征是大值很少，小值很多，所以算均值沒有任何意義。就比如圖書銷售，市場上的上百萬本圖書，前十名的每年能賣出100多萬本，而有的圖書每年賣的還不足100本。

暢銷書總是屈指可數，卻無疑是最大的贏家；無人問津的書數不勝數，卻是商業競爭的犧牲品。由于暢銷書的數量有限（即樣本很少），很難說哪些暢銷書作家是靠文筆、思想或是內容（即實力）取勝。而且實力本身也不足以解釋冪次定律現象，所以我們有必要尋找這種兩極分化現象背后的原理。

區分獨立結果和相依結果很關鍵。棒球運動員本場的比賽不受上一場成績的影響是不可能的。但是在一個賽季，這種影響就微乎其微，每場比賽可以看成獨立事件。

現在我們引入一個新的概念－路徑依賴過程，就是前面發生的事決定后面發生的事，也就是過程環環相扣。

圖：邁克爾·莫布森

這一過程的初始條件對后面的影響至關重大，比如說富人會越來越富，窮人會越來越窮。哥倫比亞大學知名的社會學家羅伯特·默頓將這一現象稱為“馬太效應”。在《圣經·新約·馬太福音》中有一句名言：“凡有的，還要加給他叫他多余；沒有的，連他所有的也要奪過來。”

假設兩名能力相當的研究生去應聘大學教授職位，一位有幸被常春藤大學錄用，另一位則被一所名氣差些的學校錄取。前者輔導的學生更優秀，教學任務更輕些，工作同事的學術水平更高，研究所得的酬勞也更豐厚。

在這種氛圍中他發表的學術論文就多，論文被引用的次數也多，名氣也就越來越大。這樣在退休時，兩人的名聲、地位就有了天壤之別。雖然馬太效應講的是同一起跑線上的兩人最后卻天差地別，但是道理卻是一樣的。

初始條件很關鍵，隨著時間的推移，微弱的優勢漸漸明顯起來。

這一現象背后有很多原理，其一就是“優先鏈接”。比如說你開發了一個新的網站，希望越來越多的人看到這個網站。最高效可行的辦法就是將新網站的網址鏈接到知名網站如谷歌、維基百科上，而不是鏈接到那些少人問津的網站。

知名網站的訪問量大，會帶來正反饋：知道新網站的人越多，訪問量就越來越大。通過優先鏈接，一些新網站的訪問量會逐漸增大，而另外的網站會因訪問量太少而被淘汰。初始的一點點優勢，就像星星之火，漸漸就形成了絕對優勢。

我們做個很簡單的模型試驗說明這一過程。假設你有一個罐子，里面裝了5個紅色彈珠、4個黑色彈珠、3個黃色彈珠、2個綠色彈珠、1個藍色彈珠。

現在你閉上眼睛，隨機摸一個彈珠。假如你摸到的是黑色的，將黑色彈珠放回罐子時再多放一個黑色的，那么罐子中就有5個黑色彈珠，其他顏色的彈珠數目不變。然后重復這一過程，隨機摸一個，放回后，再多放一個同樣顏色的彈珠。重復100次后，罐子滿了。

起初，罐子中一種顏色的彈珠越多，隨機被摸中的概率越大，比如15個彈珠中3個是黃色的，摸中黃色的概率就為20%(3/15)。

大家很容易看出這是個路徑依賴過程。如果第一次摸的是黃色彈珠，下次摸到黃球的概率就上升為25%(4/16)。不過盡管第一次摸中的彈珠顏色讓它有了累積的優勢，預測最后的贏家卻還是很難。

圖6-6顯示的是電腦三次模擬這一過程的曲線圖。第一幅圖紅色彈珠被摸到的次數最多；第二幅圖黃色彈珠最多，其次是紅色彈珠；第三幅圖的結果令人很意外，藍色彈珠最多。

你可以把不同顏色的彈珠想象成實力，數目越多代表實力越強。實力最強的彈珠得勝的概率最大，但并不能保證一定會取勝。

圖6-6

運氣將初始實力分布不斷洗牌，使得最后的結果千差萬別，難以預測。

而且一旦某種顏色一直遙遙領先，游戲就可以說結束了，因為優先鏈接已經將結果定形。雖然模型比現實生活中的事件簡單多了，但它仍然反映了在路徑依賴過程中成功和實力并沒有必然的關系。

在馬太效應中臨界點和轉折期也至關重要。轉折期中，小的累積性變導致了規模效應，這一關鍵點也俗稱轉折點。冰箱中放杯水，水會在臨界點0℃變成冰。在臨界點溫度的些許變化就會產生液體到固體的變化。社會體系中同樣存在這樣的臨界點和轉折期。

斯坦福大學社會學教授馬克·格蘭諾維特建立了一個簡單模型來演示臨界點的重要性。假設有一百個潛在的聚眾鬧事者在公共廣場上閑逛，每人都有一定的“暴動閾值”－就是鬧事者最低有多少人時他們才加入。

比如說第一個人的“暴動閾值”為零（即煽動者），后面的人為1，再后面的為2，順次延到99。這種“暴動閾值”的遞增營造了“多米諾骨牌效應”，導致暴動的發生。這就好比“破窗效應”，好事者用石頭砸了窗玻璃，很多人順次加入，最后就變成了聚眾砸破窗的鬧事。

現在我們稍微改變下初始條件：將“暴動閾值”為1的人直接換成“暴動閾值”為2的人。可以推斷，這種情況下暴動事件就不會發生了。媒體上將第一群人稱為“刁民”，第二群人稱為“良民”。而實際上，這兩類人在本質上是一樣的。僅僅是“暴動閾值”上的微小變動，就可能化暴動為和平。

上面的例子雖然很簡單，卻能讓我們明白更為現實的問題，如創新技術的應用（iPad的流行）、美國邁阿密減肥法的推行、時尚潮流的興起（如瑜伽衣），甚至疾病的傳播（如流感）。一旦小的創新有了一定的認知度，它的成功就成定局了。同理，如果形不成多米諾骨牌效應，偉大的創新也可能夭折。

在經濟學中，這種兩極分化現象常常有兩個原因：日益增長的收益和網絡效應。傳統的經濟學理論以收益遞減為根本。當一件商品供不應求時，價格會上升，生產者的收益會增加。

高額的收益吸引了大批競爭對手，他們也投入生產，最終平衡供需關系，從而使商品價格回落。這個過程就是負反饋，平衡兩極差距，使強的變弱，弱的變強。

在不同的經濟領域，負反饋不能都給人以滿意的解釋，因為正反饋往往居于上風。最經典的例子是對特定的技術確定統一的規格標準。20世紀70年代，家用錄像系統（VHS）和首款獨立盒式錄像機（Betamax）互相競爭市場份額。

近年來，索尼與松下電氣開發藍光光盤（Blue-ray）與東芝發展高分辨率光盤（HD DVD）也明爭暗斗，搶占市場。這種技術角逐是個“贏家通吃”的過程，誰占上風誰就壟斷了市場。

20世紀70年代中葉，VHS和Betamax勢均力敵，平分市場。但是VHS略占上風后，便在短短幾年內竊走了90%的市場份額。總的說來，富者越富，窮者越窮。

收益遞增總是伴隨著高昂的前期成本、低增值成本以及網絡效應（即人氣或口碑）。

微軟在個人電腦操作系統上的優勢充分體現了收益遞增的整個過程。微軟的第一代視窗系統（Windows）花費了大量的精力和時間，前期的成本非常高，但是制作附加的副本－－軟盤的成本就非常低（當時，軟件都要配置軟盤的）。因為業界標準使得人們可以進行文件交換，網絡效應對操作系統和相關的電腦程序的影響就變得很大。隨著業界標準在群眾中受到廣泛的認可，越來越多的電腦程序員開始為Windows開發軟件，這更加促進了Windows的流行。被廣泛運用的產品能給人們帶來更大的價值，因此人們對它的需求量就比較大，生產者最后的利潤也就越多。這就是需求的規模經濟。

將軟件經濟學和網絡效應結合起來，就會達到收益增值。勝利者的利潤飆升，財運勢不可擋，而初期不相上下的競爭對手卻很難分一杯羹。探討冪次效應背后的原理就是要看初始條件，關鍵的轉折期怎樣形成，看市場的兩極分化。

實力并不是在競爭中獲勝的保障，運氣才是。可以說，這些所謂的市場機制就是運氣的層層疊加。

海量資訊、精準解讀，盡在新浪財經APP