摘   要

　　通脹水平是影響商業銀行資產配置和交易決策的重要因素。春節作為我國重要的傳統節日，會因春節效應和春節錯位等因素對通脹水平產生影響，并給債券市場帶來短期沖擊。本文基于單變量模型進行預測，并結合2010年以來1月、2月居民消費價格指數的變動情況，分析了春節因素造成的預測誤差，對預測值提出了調整建議，最后對2024年春節通脹水平進行了預測。

　　關鍵詞

　　CPI預測　單變量模型　春節效應　春節錯位

　　居民消費價格指數（CPI）是衡量我國通脹水平的核心指標，受到宏觀調控部門、金融機構、企業等各界的廣泛關注。對于債券市場投資者而言，一方面，通脹的走勢會影響交易投資決策，進而決定債券的中長期走勢；另一方面，在債券交易實務中，因為指標的實際公布值（以下簡稱“實際值”）和市場預測值（以下簡稱“預測值”）之間時常形成預期差，CPI、社會融資規模等經濟金融指標的月度發布往往對市場造成短期沖擊。因此，對指標的精確預判，是有效把握債券市場交易機會、管理市值波動風險的重要基礎。

　　在實踐中筆者發現，春節作為我國重要的傳統節日，對CPI有著顯著影響（即春節效應），也經常出現實際值與預測值差異較大的情況，給債券市場帶來短期沖擊。為了幫助投資者優化交易決策，本文使用量化模型對通脹指標尤其是春節期間的通脹指標進行建模和預測，以期為市場提供預測基準參考。

　　通脹指標量化預測的基本方法

　　（一）建模方法選擇

　　單變量模型是預測宏觀指標的一類簡明而經典的方法。該方法的基本假定是數據已包含全部歷史信息，僅采用指標數據即可建立模型。模型結構簡明，并且在樣本內估計和樣本外預測維度下的評估均有較好表現，在經濟指標預測方面被廣泛使用。因此，本文使用單變量模型預測CPI，其核心表達式為：

　　式（1）中，

　　t期CPI所包含的全部歷史信息，F（·） 表示單變量函數，εt為模型殘差項。

　　t期對未來第t+h期指標的預測值，

　　其中：

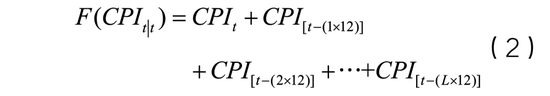
　　式（2）中，

　　t期起，向歷史回溯L年的月度數據。根據建模的目標，L年可以選擇為3年、5年等中短周期，也可以選擇10年甚至更長時間的長周期。

　　本文討論CPI模型的近端預測，即使用第t期模型和數據完成對未來第t+1期的預測。對于CPI這類具有季節性特征的時間序列數據，使用單變量方法建模在近月預測中平均誤差小，且預測精度表現穩定。綜合考慮模型特點和數據特征，本文選用單變量模型作為預測通脹的基本方法。

　　（二）CPI模型的相關設定

　　我國公布的CPI相關指標主要有三種形式：環比增速、同比增速和定基指數，功能包括監控指標的波動、變化趨勢以及這些變化的積累發展情況。同比增速和環比增速使用得較多，指標實際值的數據精度相同（均保留到小數點后一位）。筆者通過實驗發現，在指標數據精度相同的前提下，數據數量級越小，預測誤差越小，預測精度越高。因此，選擇數量級最小的環比增速指標用于預測，再通過指標之間的數量關系，由環比增速推導得到對同比增速的預測，以獲得較好的預測精度。推導公式為：

　　在選定CPI單變量模型的環比增速作為預測指標后，如何選擇訓練樣本的長度，是所有使用“一串連續的數據”來訓練模型的過程中必須面對的一個問題。首先，訓練模型需要大樣本，長度包括至少一個能滿足預測的完整周期（對CPI而言需要3到5年的歷史數據）。同時，由于模型用于環比指標的外推預測，為了較充分地捕捉短期波動的特征，訓練樣本長度也不是越大越好。綜合上述分析，筆者選擇近5年（L=5）的CPI數據建立單變量模型，預測CPI環比增速。

　　春節效應和春節錯位因素的主要表現

　　（一）春節效應的具體表現

　　歷史經驗顯示，春節效應對于CPI環比增速、同比增速的影響均比較顯著。

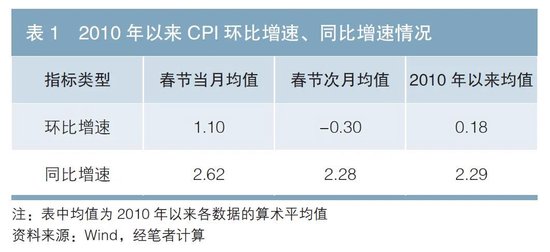
　　春節效應對CPI環比數據的沖擊比較容易理解。在居民置辦年貨、餐飲囤貨、節日送禮等需求拉動下，春節當月的CPI環比數據基本位于全年較高水平。隨著春節效應的消退，在前月較高基數的壓力下，春節次月的CPI環比數據會降至全年較低水平。如表1所示，2010年以來春節效應在CPI環比數值中有明顯體現。其中，春節當月平均環比增速為1.10%，遠高于月度平均水平（0.19%）。春節次月漲價效應退潮，平均環比增速跌落至-0.30%，明顯低于月度平均水平。

　　春節效應對CPI同比增速的沖擊主要來自兩方面。一是與環比增速類似，春節前后消費火爆，形成的短期波動對春節當月的同比增速也形成拉動；二是當年同比增速的較高水平使得次年同月的同比增速面臨較高的比較基準，容易產生波動。

　　（二）春節錯位的主要表現

　　春節假期的公歷日期有時在1月，有時在2月，如果相鄰年份的春節日期落在不同月份，則出現春節錯位現象。具體來看，春節錯位的情形包括當年春節在1月、上年在2月（情況1），以及當年春節在2月、上年在1月（情況2）兩類（見表2）。其余情況可定義為正常年份，無錯位情況。

　　由于上年同期基數未對齊，春節錯位因素常導致1月、2月CPI的同比數據波動加大，實際值與預測值之間也經常存在較大差距。而1月、2月的通脹數據是債券市場全年運行中樞的關鍵觀測月份，對全年的通脹水平有重要指示作用。有鑒于此，筆者擬通過研究CPI通脹模型在春節錯位因素影響下的預測表現，針對兩類春節錯位情況提出預測調整方向，以更好地預測相關數據，以及應對春節期間的債券市場價格的調整風險。

　　春節錯位因素對CPI預測的影響及建議

　　筆者使用單變量模型對2020—2023年的通脹增速進行預測，對上文的判斷進行驗證，結果發現，在春節當月前后，模型的預測準確性的確會受到短期沖擊。為理解進而改善模型在春節前后的預測效果，筆者使用2010—2023年的歷史數據，分析春節錯位因素造成的預測偏誤。同時，對受到影響月份（主要是春節所在的1月、2月）的單變量模型預測結果提出調整建議。

　　（一）2010年以來的春節錯位情況

　　逐年來看，在2010—2023年的14個春節中，有10年出現春節錯位情況，占比超七成。其中，2012年、2014年、2017年、2020年及2023年為情況1，2010年、2013年、2015年、2018年及2021年為情況2，其他為正常無錯位年份。

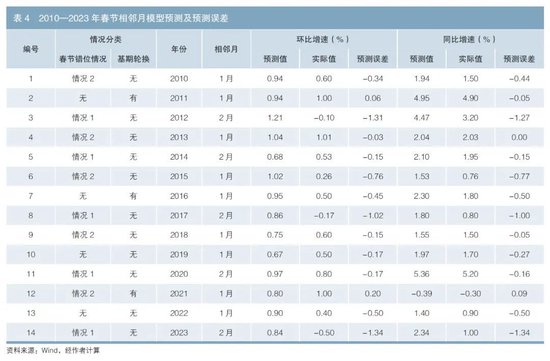
　　春節錯位對預測精度的影響主要體現在春節當月及相鄰月，所以可以將錯位情況分為兩類討論：對于春節錯位情況1，定義1月為春節當月，2月為春節相鄰月。對于春節錯位情況2，則定義2月為春節當月，1月為春節相鄰月。表3列示了2010年以來春節當月CPI環比增速、同比增速的模型預測值及預測誤差（實際值減預測值），表4列示了春節相鄰月的模型預測值及預測誤差。

　　同時，CPI數據指標每5年進行基期輪換，以末尾數字逢0、逢5的年份作為新一輪的統計基期。所以，基期輪換會對逢1、逢6年份的CPI數據造成影響。為了獨立分析春節錯位因素對預測的影響，本文在后續分析春節錯位因素造成的預測誤差的時候，不考慮受基期輪換影響的2011年、2016年和2021年的情況。

　　（二）春節錯位對CPI預測的影響分析及調整建議

　　從表3所列示的預測誤差來看，春節當月CPI環比增速模型預測值低于實際值的情況較多，即模型存在低估情況。因此，可在模型預測值的基礎上適當向上加點進行調整。預測誤差較集中地落在（0，0.6%）區間，向上調整幅度的參考值可選在0.3%左右。其中，情況1的環比增速調整幅度較情況2要高，可將情況1的環比增速調整值設為0.4%，將情況2的環比增速調整值設為0.2%。

　　從表4所列示的情況來看，春節相鄰月CPI的環比增速模型預測值高于實際值的情況較多，即模型存在高估情況。因此，可在模型預測值的基礎上適當向下減點進行調整。預測誤差多數落在（-1.2%，0）區間，向下調整的參考值可選擇-0.6%左右。其中，錯位情況1的環比調整幅度相對更大，可將情況1的環比增速調整值設為-0.9%，將情況2的環比增速調整值設為-0.3%（見表5）。

　　對2024年春節通脹水平的展望

　　2023年春節為1月22日，2024年春節為2月10日。根據前文分析，僅考慮春節錯位影響，2024年1月CPI同比增速更可能出現負的預測誤差，2月更可能出現正的預測誤差，分別可能對10年期國債收益率產生向下（利好多頭）和向上（利好空頭）的日內短期沖擊。根據實際需求及業務策略，建議債券市場參與者提前作出安排，并適當把握通脹數據公布前后的交易機會。

　　筆者基于前文所述方法對2024年春節的CPI數據進行具體預測。首先，依據截至2023年11月末的統計數據，單變量模型對2024年1月、2月CPI環比增速的預測值均為0.80%，對應的同比增速預測值分別為0.2%、1.6%。其次，依據春節錯位情況分類，2024年春節錯位屬于情況2，所以應向下調整2024年1月的環比增速預測值，并向上調整2024年2月的環比增速預測值。最后，通過計算得到2024年1月、2月對應的CPI環比增速調整結果分別為0.5%、1.0%，同比增速調整結果分別為-0.1%、1.5%。

　　需要注意的是，雖然近兩年CPI預測未受到數據基期輪換因素的影響，但考慮到2023年1—2月正處于優化調整疫情防控政策的關鍵節點，該因素對2023年及2024年的CPI預測值均有影響，亦應加以謹慎考慮并適當調整。其中，2023年1—2月經濟逐步復蘇，但居民消費尚未全面恢復；2024年為優化調整疫情防控政策后的第二個春節，居民消費增長動能有望持續轉強。因此，在春節錯位的基礎上綜合考慮，預計2024年1月、2月CPI環比增速的所在區間分別為（0.4%，0.7%）（0.8%，1.2%），2024年1月、2月CPI同比增速的所在區間分別為（-0.2%，0.2%）（1.2%，1.9%）。此外，還可根據2024年春節旅游、服務消費、備貨送禮需求等具體情況再適度調整，以便獲得更加精準的預測值。（本文僅代表作者個人觀點，不代表所在機構觀點和立場）

　　參考文獻

　　[1]董德志，李智能． CPI非食品環比“高頻+均值”預測方法研究[J]． 債券，2015（8）．

　　[2]何曉群． 多元統計分析[M]． 北京：中國人民大學出版社，2019（6）．

　　[3]梁詠梅，董敏杰． 月度CPI增速的高頻數據預測方法[J]． 當代財經，2018（12）．

　　[4]路思遠． CPI構成項目權重估算及2016年走勢預測[J]． 債券，2016（4）．

　　[5]肖爭艷，陳彥斌． 中國通貨膨脹預期研究：調查數據方法[J]． 金融研究，2004（11）．

　　[6]熊偉琪，張鵬． 穿越周期的通脹預測：季節性模型及高頻數據的適用性[J]． 金融市場研究，2021（6）．

　　[7]中國人民銀行調查統計司． 時間序列X-12-ARIMA季節調整——原理與方法[M]． 北京：中國金融出版社，2006．

　　[8] SWANSON N R， XIONG W Q， YANG X Y． Predicting Interest Rates Using Shrinkage Methods， Real‐time Diffusion Indexes， and Model Combinations[J]． Journal of Applied Econometrics， 2020， 35（5）．

　　◇ 本文原載《債券》2023年12月刊

　　◇ 作者：中信銀行總行金融市場部　熊偉琪　張鵬

　　◇ 編輯：涂曉楓　劉穎

海量資訊、精準解讀，盡在新浪財經APP

責任編輯：趙思遠