意見領袖 | 王劍

　　我們繼續探討銀行股的低估值之迷，這個老生常談的話題。這問題研究了好幾年了，低估值現象一直持續，未見改觀。

　　01

　　股息折現

　　我們依然先從經典的股息折現模型出發。銀行股的價值（P）是其未來股息（D）的折現：

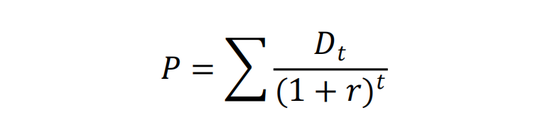
　　股息折現模型邏輯簡單直白，易于理解。但這模型有一個硬傷，就是對銀行股未來很遠的股息，其折現值占最終的估值結果（P）的比例很高。比如，我們使用股息折現模型時，一般會對銀行股未來的經營分2-3個階段進行預測，越是后面的階段，離現在越遠，預測越不靠譜。

　　比如，我們此前使用過一個虛擬的銀行來演示股息折現法，該行的預測為：

　　基于上述預測，使用10%的折現率，得到2019年底的銀行價值為125元。而如果我們把三個階段各自的股息折現加總，則分別是18元、34元、73元，分別占總估值125元的14%、27%、58%。所以，越是靠后的階段，也是越不可靠的階段，在估值結果中的占比反而越高，這也是股息折現模型的一大缺陷。

　　之所以出現這一缺陷，是因為股息折現模型的邏輯是：將銀行的現有凈資產視為沉沒成本，而將未來的現金流入視為價值所在。但事實上，銀行現有的凈資產也是屬于股東的真實財富，徹底將其視而不見也不太合理。

　　02

　　EVA折現

　　因此，可以換一種思路。新思路為：將銀行凈資產也視為股東所擁有的財富，是真金白銀；然后，將這筆凈資產未來所能產生的價值——用經濟利潤（EVA，又稱經濟增加值，即利潤中超過股權成本的額外部分）來衡量——折現，凈現值加總。凈資產與EVA現值之和，即為銀行的總價值。

　　EVA估值模型的結果，銀行的凈資產存量價值占總價值的比例較高，遠期EVA現值的占比低一些，能夠有效克服股息折現模型的缺陷。當然，它也有自己的問題。

　　理論上，股息折現模型和EVA折現模型是等價的。當然，這只是理論上。我們用虛擬的銀行例子來說明其兩者的關系。首先是一家凈資產為B，每年盈利能力為ROE，并將全部利潤用于分紅的銀行。其每年的凈利潤、股息為：B·ROE。

　　其中，（ROE-r）B 就是EVA。

　　因此就得到了EVA折現模型：

　　這樣，銀行的價值就體現為了兩部分：凈資產，外加未來創造的EVA的折現。

　　這個公式也很直觀地推導出了PB（在上式兩邊除以B）：

　　一家銀行有沒有破凈，就是ROE和折現率比大小。如果ROE還不如自己的折現率高（意味著EVA為負數），那么投資于這樣的銀行股當然是毀滅價值的，就該破凈交易。

　　如果考慮一個分紅比例（d），而不是將凈利潤全部分紅，那么其結論也是類似的。在這種情況下，銀行的凈利潤、凈資產（B）、EVA會以g=ROE（1-d）的速度在增長（假設ROE長期不變）。其股息折現模型為（式中B、EVA均為第一期的B、EVA）：

　　同樣可得轉換為EVA折現模型：

　　凈利潤部分分紅情況下的EVA折現模型為：

　　顯然，若EVA為負數，則P小于B，即銀行股破凈。這一點結論和全分紅情況下是一致的。也就是說，如果B沒問題，那么導致破凈的原因就是EVA 為負，即銀行創造利潤的水平還不如折現率，那么這種資產是消滅價值的。

　　03

　　清算價值

　　接下來就得討論一個問題：B真的沒問題嗎？B的最大問題是，它用的是會計上的歷史賬面價值。

　　一方面，如果有隱藏的不良資產尚未確認，那么B就是虛高的。那么就很容易解釋PB小于1。比如PB=0.9，股價是9元，B是10元，但其實B是虛高的，剔除掉隱藏的不良資產后，真實的B只有9元，那么這銀行的真實PB其實是1倍。

　　這種觀點是銀行股輕微破凈的那幾年較為流行的。但隨著這幾年PB繼續下行，其解釋力明顯不行了。因為，現在很多銀行的PB已經掉到0.5倍以下，假設真實PB是1倍，那么倒算出來的隱藏不良資產非常夸張，可能高達20%多。而很多低估值銀行的資產質量不可能差到這個程度。因此，隱藏不良資產不足以解釋過低的PB。

　　我們先不考慮資產質量風險。

　　此時，影響B的，還有另外一個因素：B的公允價值與其歷史賬面價值的偏差。公允價值是指該資產的未來現金流按最新的利率進行折現，由于利率會變化，所以最新的公允價值會偏離原來的賬面價值。

　　一家銀行的B是其資產價值與負債價值之差。銀行財務報表上的資產價值、負債價值是按歷史計賬的。銀行的資產、負債一旦確定名義利率后，日后遇上利率發生變化，那么其公允價值就會發生變化。

　　我們依然從股息折現模型出發。銀行價值是未來股息的折現，為P。但如果按最新的市場利率折現，計算出銀行凈資產的公允價值，記為M，M與P有偏差（因為兩次折現的利率不同）。我們先來理解一下這個偏差（P-M）。

　　P是凈資產的合理估值，而M是按當時的利率算出來的凈資產的公允價值。M的意思是：如果你現在清算了這家銀行，將其貸款、存款按當時的市場利率進行出售，那么能夠凈收回資金M。所以這M也可稱為“清算價值”。但很顯然，銀行股票在市場上交易，不會按這個M的價格來交易，而是會偏離。我們可以將偏離理解為：這家銀行此刻不清算，那么這個“不清算”的行為等價于（還是借用EVA估值模型的思維）：既然清算能得到M，那我此刻不清算，就等于是用M元的資金買下這筆資產，然后這筆資產將來能為我創造更多EVA，將未來的EVA折現，得到一筆現值。這筆現值與M之和，就是P。

　　04

　　特許價值

　　所以，P-M代表的是：銀行此刻不清算，而讓它繼續經營，所能產生的未來的EVA的現值之和。未來的EVA現值，我們稱為銀行的“特許價值”。

　　當然，有些銀行可能未來能產生的EVA是負的（是消滅價值的），所以P-M小于0，即股價交易于M以下……

　　因此，P可以分解為M和特許價值。

　　P=清算價值（M）+特許價值

　　更精準的算法如下。我們假設一筆資產的歷史面值為A，名義收益率為a，但后來利率發生變化，現在同類資產的收益率已變為a’（市場利率）。投資人的折現率仍為r。

　　為簡化，我們假設該資產只有兩期。

　　那么，該資產的價值P是其未來現金流的折現：

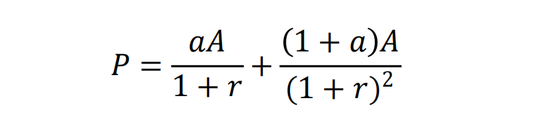
　　但由于市場利率已經變為a’，如果資產持有人想提前變現該資產，可能沒辦法以P的價格賣出（P是按投資人自己的折現率r算出來的），只能按以下價格賣出：

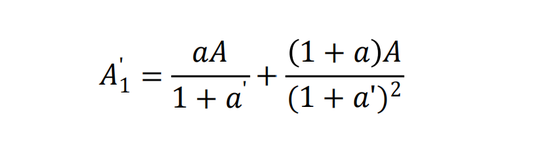
　　這個 A‘1 就是清算價值（M）。P - A‘1 即為特許價值。

　　如果過了一期，到了下期末，到時候再賣出，則賣價如下（最后一期的現金流入，按a’折現），也就是下期末的清算價值：

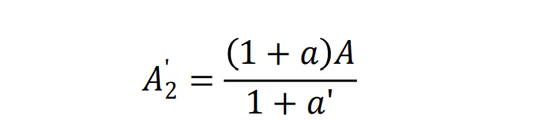
　　該模式還能納入不良資產的考慮。比如，如果能夠估計出不良貸款率是n（假設，最后償還時會損失比例為n的本金，但利息能夠償付），那么：

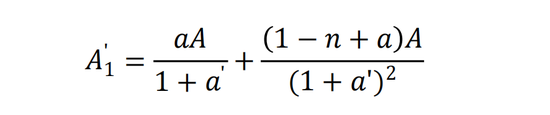
　　下文先不考慮不良資產。

　　以下會通過一個繁瑣的推導，求出特許價值：

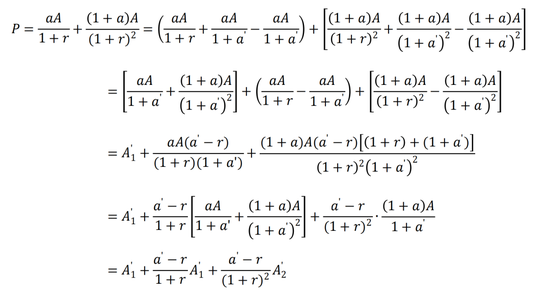
　　即

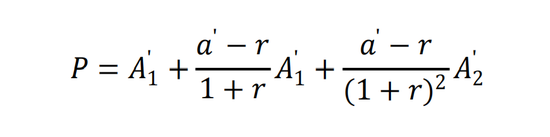
　　如果是無限期，則是：

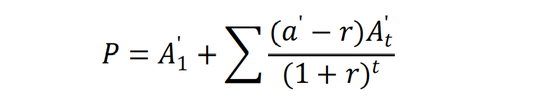
　　這是一個和EVA折現模型非常相似的公式，其含義為：股票價值，分為兩部分， A‘1 是按公允價值計量的凈資產，即清算價值（M），而后面是特許價值，是將 A‘1 投入經營后，未來每年能產生的EVA的折現值。

　　其中，EVA的算法是，以 A‘t 為本金投入生產，其收益率是a’，而a’超出r的部分，即為剔除股權成本的額外收益，再將其乘以本金 A‘t ，得到EVA。我們可將其標為EVA’，以示區別。于是：

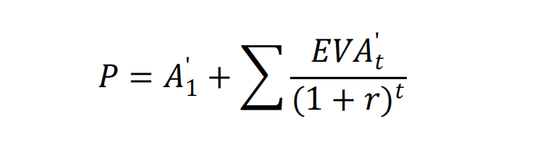
　　05

　　估值進階理解

　　我們將上面兩種EVA模型寫在一起：

　　理論上，上述兩個公式算出來的P應該是一樣的。兩者只是對凈資產的定價不一樣。當然，理論上使用凈資產的清算價值更合理一點，畢竟它考慮了凈資產現在的市場價值。

　　但不管如何，EVA模型的目的是：把銀行股的價值，劃分為“凈資產價值”和“未來持續經營能產生的特許價值的折現”兩部分。講得更通俗一點，是“現有的價值”和“未來能產生的價值”兩部分。

　　精通保險股估值的朋友，應該很容易接受這一思路。因為保險股的內含價值估值法也是這一思路。

　　凈資產能代表“現在的價值”，這是金融企業的優點之一。因為，金融企業的資產主要是金融資產（我們一般不會考慮其持有的固定資產的價值，比如樓宇），理論上是可以轉換為現金的，比如通過上面的清算價值。這不像一些工業企業，其資產主要是固定資產或專有設備，轉換成現金的難度很大（有些專用設備幾乎沒有流動性，其清算價值只能是廢舊金屬回收的殘值）。對于這樣的企業，運用EVA模型似乎不太合適，那么使用股息折現模型更合適。對金融企業而言，將凈資產（尤其按公允價值）視為現金，視為現有的價值，是可行的，所以可以用EVA折現模型。

　　劃分為“現有的價值”和“未來能產生的價值”兩部分，有助于我們去思考銀行股低估的根源。其中， A‘1 部分已經考慮了利率變化和不良資產導致的公允價值變動（即考慮了利率風險和信用風險。如果兩類風險都不大，那么 A‘1 和B相近），而剩余部分就是特許價值。現在很多銀行股嚴重破凈，也就是P顯著小于現有的價值，意味著其特許價值為負，即未來它是在消滅股東價值的。

　　這也就是我們此前的觀點：銀行股低估的原因，是其特許價值的破壞。

　　(本文作者介紹：中國人民大學金融學碩士，CFA持牌人，曾供職于浙商證券、光大證券研究所，擔任金融行業分析師，2018年加盟國信證券，任金融業首席分析師。)