來源：量子位

一盆熱水放著就會逐漸變冷。

在這背后是一條著名的物理學法則——熱力學第二定律：熱量不能自發地從低溫物體轉移到高溫物體。

舉個最簡單的例子：不做任何干預，把一冷一熱兩個鐵塊貼在一起，熱的鐵塊會迅速將熱量傳給冷的鐵塊，最終達到相同的溫度。

也許你會說，空調和冰箱都是讓熱量逆向傳遞了啊。

其實，空調和冰箱實現制冷的前提也是依靠壓縮機做功，并不能讓熱量自覺從低溫部分轉移到高溫部分。

不過你知道嗎？

其實在150年前，就有科學家找到了熱力學第二定律的bug！

這就是大名鼎鼎的麥克斯韋妖（Maxwell’s demon），由著名物理學家麥克斯韋提出。

現在，居然有人把這個妖精造了個新版本出來，而且還是個“賭徒版”的！

什么是麥克斯韋妖？

看到妖字，你可能在想：

怎么科學界還搞牛鬼蛇神？

其實這只是一個假設。

麥克斯韋設想，將一個裝有氣體分子的盒子，用擋板隔成兩個部分，在擋板上設置一個非常小的門，假設有一個非常非常小的妖精把守門口。

氣體分子速度有快有慢，我們可以把它們分成兩類：一類是速度比較慢的“冷分子”，一類是速度比較快的“熱分子”。

于是，這個“麥克斯韋妖”就蹲在門口附近觀察，如果左邊有“冷分子”撞過來，就把門打開，讓它過去，然后快速關上門。

同理，它也會把“熱分子”釋放到左邊去。

這樣經過一段時間反復操作后，左邊只有“熱分子”，右邊只有“冷分子”。

因為麥克斯韋設想的妖精非常小，門也非常輕，因此做功可以被忽略不計。

那么矛盾就來了。

麥克斯韋妖居然不怎么做功就實現了熱量的逆向流動，熱力學第二定律居然被推翻了？

熱力學第二定律顯然是對的（否則就能造出永動機），那么麥克斯韋設想的妖怪究竟在哪里出了問題？

一種觀點認為，測量分子的速度會消耗能量，從而導致系統“熵增”，其實這沒有觸及到問題的本質。

直到香農提出了信息論后，“麥克斯韋妖是一個悖論”才變成了板上釘釘的事實。

1948年，著名數學家香農證明了信息是可以被量化的，并提出了“信息熵”；

在此基礎上，1961年德國裔美國物理學家羅爾夫·朗道爾(Rolf Landauer)提出了Landauer原則。

他認為任何抽象信息都必須有物理載體，對信息的操作就意味著對物理載體的操作，而對信息的處理有些是邏輯不可逆的，因此也就會伴隨著熱力學上的不可逆。

朗道爾認為，在平衡態下擦除1bit的信息，至少要消耗的能量為kTln2 (k為玻爾茲曼常數，T為環境溫度)。

換而言之，改變1bit香農熵所需的最低能量，是kTln2。

但什么是邏輯不可逆呢？

這是指多種不同的輸入會對應同一個輸出，比如擦除信息就是不可逆的，因為它會把所有的信息都輸出為擦除這一個狀態。

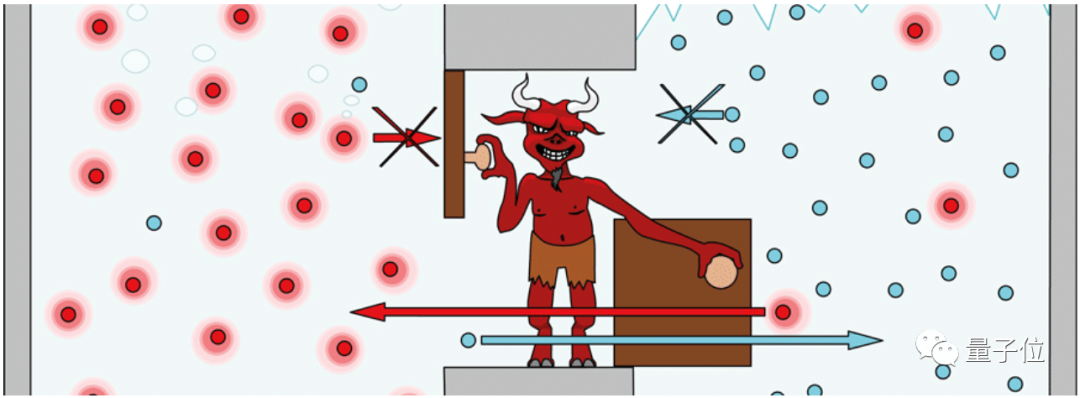
1982年，美國物理學家查爾斯·班尼特（Charles Bennett）將這些概念綜合在一起，提出：麥克斯韋妖的核心是一個信息處理器。

它需要記錄和存儲關于單個粒子的信息，以便決定何時開門、關門。并且它需要定期刪除這些信息，清一下“內存”。而根據“擦除”原理，擦除信息回帶來熵的增加，將遠遠超過粒子分選所引起的熵減。

終于，從提出后經過了115年，麥克斯韋妖被證明是悖論，熱力學第二定律也因此更加完善。

不過科學家們可沒有就此作罷，他們對這個“小妖精”一直熱情不減。

雖然最終麥克斯韋妖并不違反熱力學第二定律，但是我們有沒有可能造出真正的麥克斯韋妖呢？

進入21世紀后，大家真的開始試著在實驗室造“妖”了！

最早在2007年，科學家們用一種光能門，實現了一種麥克斯韋妖系統：

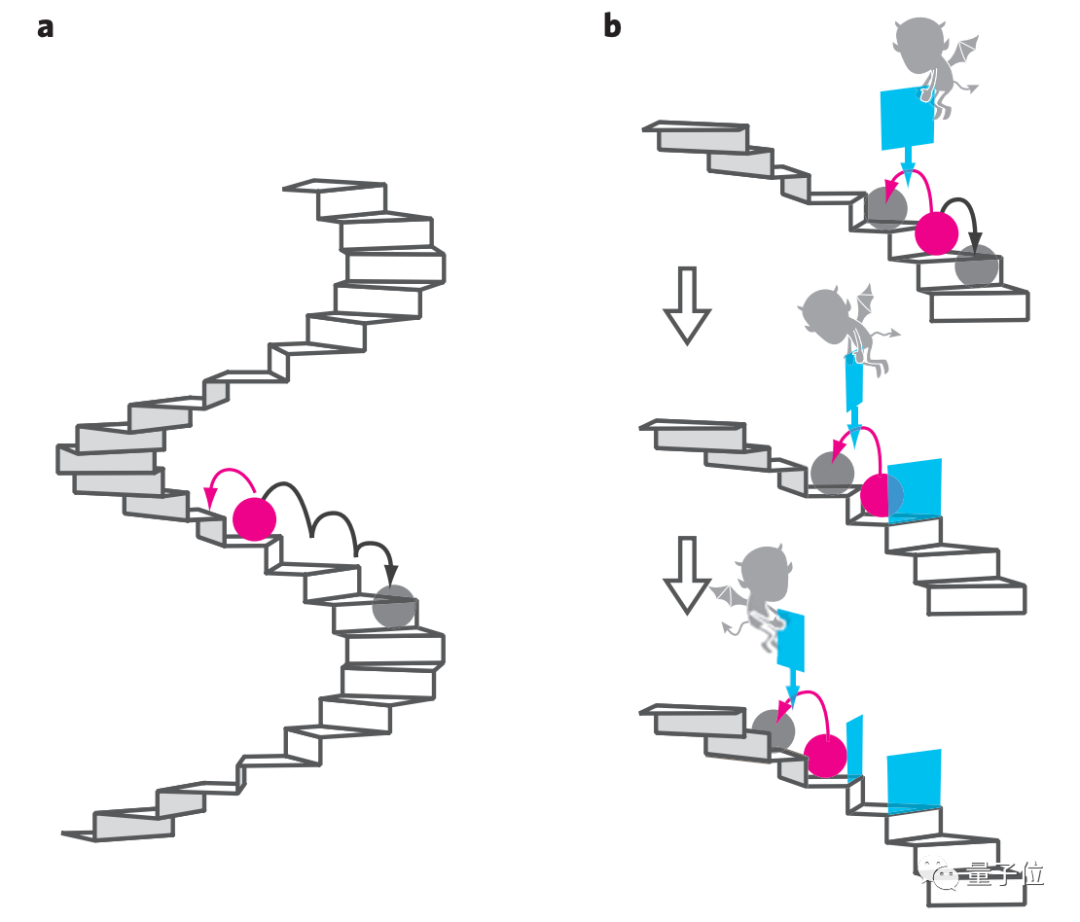
2010年，日本物理學家在《Nature》發表了一篇論文，以西拉德發動機概念為基礎，研究出了如何將納米級珠子誘導上螺旋樓梯的方法。

2013年，德國科學家用一對相互作用的量子點(只有幾納米寬的微型半導體)建造了一個麥克斯韋妖實驗裝置。

△賓西法尼亞州立大學的科學家將隨機原子陣列重新排列成有序的原子塊

2018年，來自賓夕法尼亞州立大學(Penn State)的物理學家們，將隨機排列的原子重新排列成有序的原子塊，創造了一個量子意義上的麥克斯韋妖。

“賭徒版”麥克斯韋妖

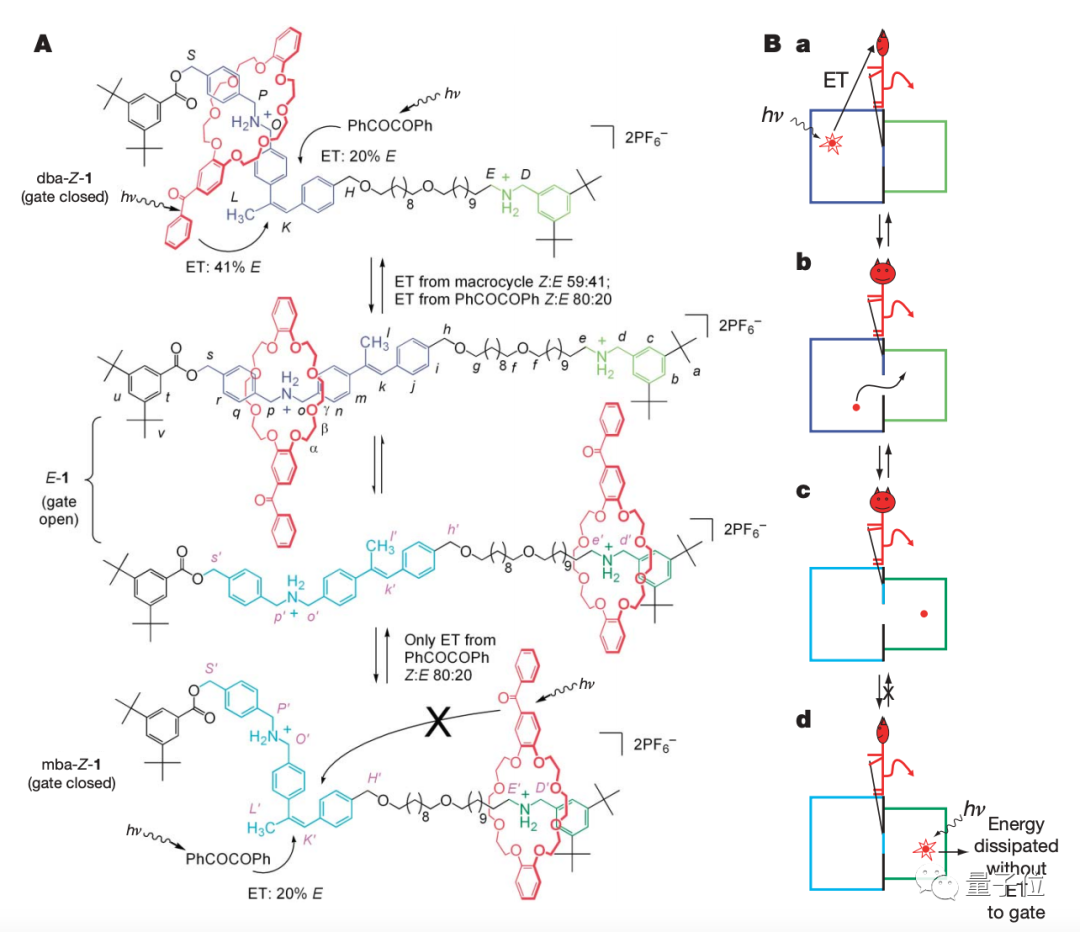
然而，這些年提出、以及實現的各版本麥克斯韋妖，還是太復雜了。

無論是用化學粒子、還是用光子實現，本質上都是在重復用信息換能量的過程。

也就是說，麥克斯韋妖需要掌握門板兩側的粒子信息，來決定是否開關門板。

有沒有一種辦法，來搞出一個“手頭上沒有任何信息”的麥克斯韋妖？

它會不時消耗一點能量，來看看系統有沒有“獲取能量”，并決定要不要繼續這一過程。

如下圖，W是麥克斯韋妖消耗的能量，而F是系統可能獲得的自由能量（隨著門板開關，恰好成功分離了冷熱粒子）。

它看不見系統里的狀態，因此沒辦法控制門板的開關，只能憑直覺選擇要不要繼續拿W賭F。

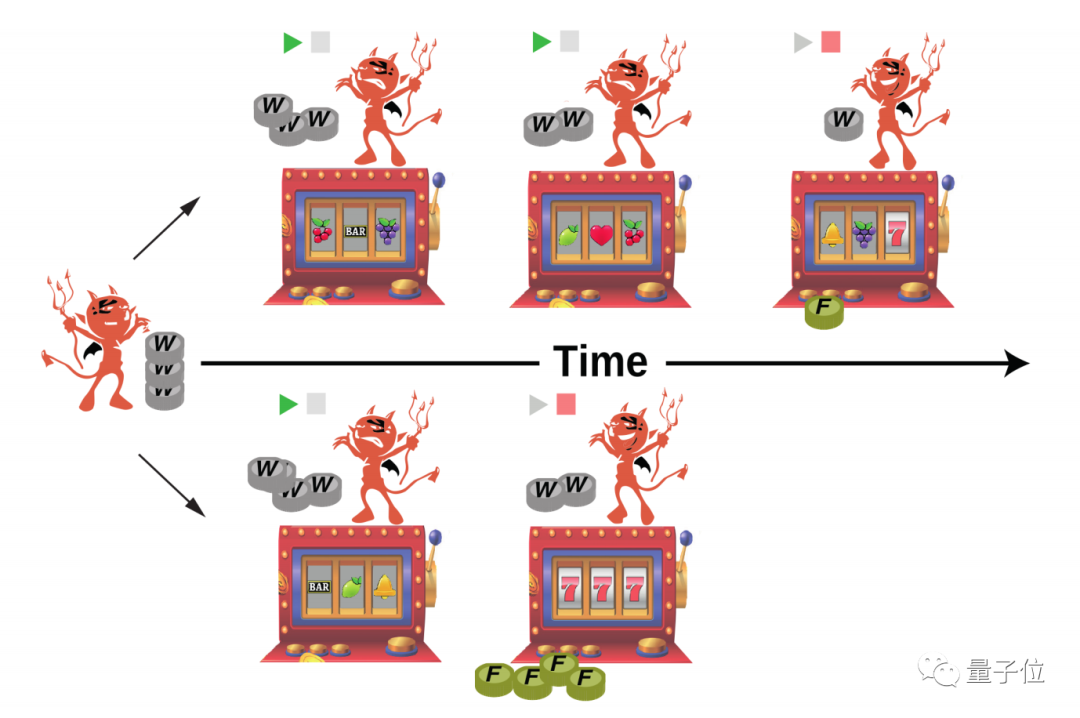
沒錯，這樣的麥克斯韋妖，就是一個徹底的“賭徒”——

它不知道系統下一刻的狀態，也不知道自己消耗的能量能否換取更多自由能量，所能做的只有靠“猜”。

這個新版“妖精”，看整個系統的眼神，就像是在看一個賭桌游戲——

這局輸（沒有獲得能量）的話，下一局還會輸嗎？要是我停止賭（消耗能量）的話，能及時止損嗎？

這會出現兩種情況：

其一，消耗的能量太多，超過了一個閾值。這時候，麥克斯韋妖就會“啪”一下離開賭桌：不玩了！

其二，只用極少的能量消耗，麥克斯韋妖就獲得了巨大的自由能量（無意間分離了大量冷熱粒子），那么它也可以選擇立即結束游戲：狠賺一筆！

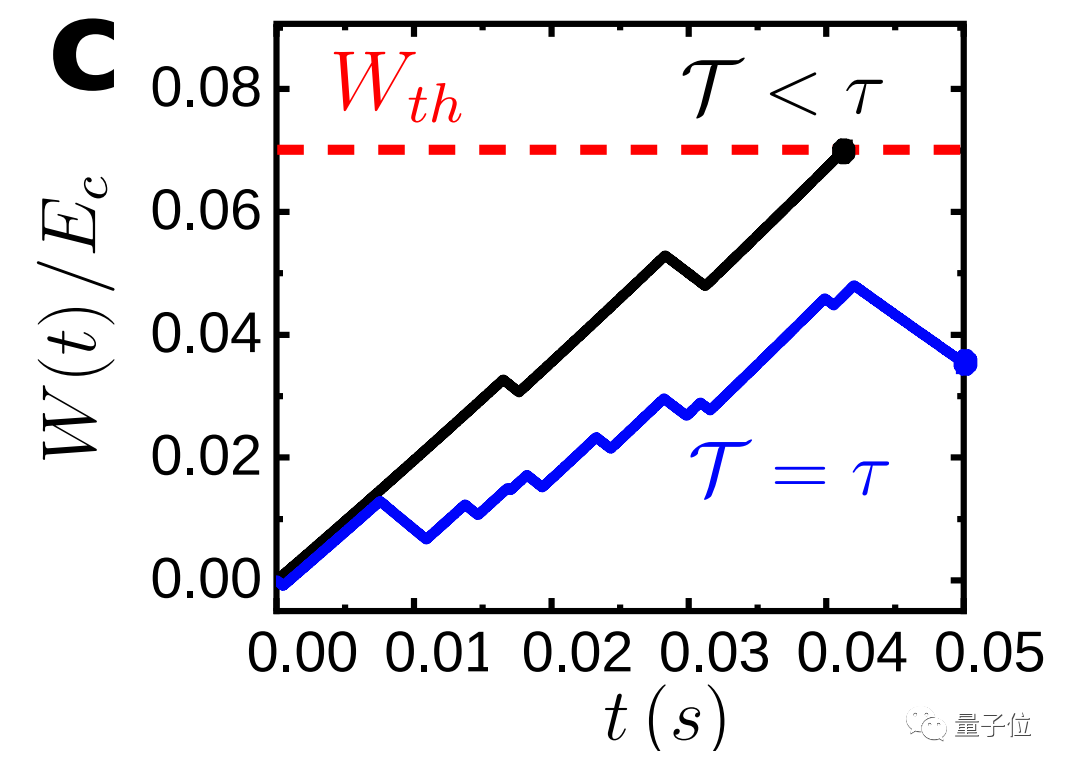
如果出現第二種情況的話，實際上就短暫地顛覆了熱力學第二定律——消耗少量能量，來換取更多的自由能量。

對于這種現象，來自國際理論物理中心ICTP的物理學家、作者之一édgar Roldán解釋：

這就像你既可以在賭桌上玩一整夜，也可以在贏了100美元后立即停手。

當然，最重要的是，現在科學家實現了這個“賭徒版”麥克斯韋妖。

如下圖，他們搞出了一個由電極（淺藍色）和銅島（紅色）組成的系統。

當設備冷卻到只比絕對零度高出一點點（約幾分之一開爾文溫度）時，單個電子就可以實現在電極和銅島之間“反復橫跳”。

其中，從電極到銅島上是消耗能量的過程；而從銅島到電極，就是獲取能量的過程。

在此期間，中間那個藍色的靜電計能隨時測量兩邊的電量，這就做出了一個“賭徒版”的麥克斯韋妖——

期間，系統可以隨時被停止，也可以繼續下去，一切都取決于麥克斯韋妖的判斷。

研究者們認為，這一系統仍然能被用于提升微觀熱機和發動機的性能。

“久賭必輸？”

但別忘了，熱力學第二定律是一個基于統計學得出來的規律。

也就是說，雖然這個“賭徒版”麥克斯韋妖，能偶然打破熱力學第二定律，但在長期統計下，是不可能一直打破熱力學第二定律的。

有網友表示，自己已經看破了這個“賭徒版”麥克斯韋妖的小伎倆：

這不就是N=1和N=1000之間的差異？如果只做一次實驗，確實可能偶然顛覆這一定律。畢竟根據“賭徒定理”——久賭必輸嘛。

頓時有網友陷入了迷思：

要是掌握（賭博）技巧，是否就能超越極限？

不。

論文第一作者、來自國際理論物理中心ICTP的物理學家Gonzalo Manzano表示：

“賭徒版”麥克斯韋妖成功的方法之一，就是在事情變壞的一剎那，及時止損，以避免更巨大的損失。

連物理學家都如此勸誡，賭博這個東西，確實別沾為妙（手動狗頭）。

（聲明：本文僅代表作者觀點，不代表新浪網立場。）