當各位小伙伴搭上回家的公交車、地鐵甚至高鐵,拿出手機,開始安心的進入坐享行程模式時。有可能你會遇到這種情況,我的天啊,速度為300km/h的高鐵上竟然也有蚊子?
動了動聰明的小腦瓜,計算了一下,此時的蚊子豈不是正在以83m/s的速度相對于地面運動?那好奇的小伙伴就問了,它到底會不會因為高鐵的加速而被甩到車尾?
下面,我們來解釋這些問題,還有更多奇葩的腦洞問題,閱讀全文了解一下吧!
最近某視頻軟件上,一個看似和物理有關的問題火了:高鐵上的蚊子到底會不會因為高鐵的加速而被甩到車尾?

看了眾多博主對此的解釋,小編這個人間清醒,啪的一下就站起來了 ── 看似簡單的問題其實里面其實包含了非慣性參考系、流體力學等方面的知識。

在開始正式推導之前,先擺出我們的結論。在一直加速的列車廂內(nèi),蚊子只保持懸浮狀態(tài)的話確實是會甩到車后!只要車廂夠長,蚊子就會相對車廂向車廂后做勻速運動。
具體的約束條件還有一些推論,比如:“蚊子的受力是怎樣的?”、“蚊子什么情況下會撞在車廂前壁?”、“如果車廂被我們抽成真空,會有什么不同?”等,我們會在后續(xù)的推導中進行闡述。
問題背景
很多小伙伴有過這樣的體驗,當搭上回家的公交車、地鐵甚至高鐵,拿出手機,開始安心的進入坐享行程模式時。有可能你會遇到這種情況,我的天,高鐵上竟然也有蚊子?你會不會瞬間帶上痛苦面具,露出下面的表情?
不過速度為300km/h的高鐵上的蚊子,此時豈不是正在以83m/s的速度相對于地面運動?
了解相對性原理的同學,肯定能知道這只是參考系的問題。車廂,車廂內(nèi)的空氣和蚊子,相對靜止,以車廂為參考系,蚊子在車廂內(nèi)就如“飛”平地。勻速階段也不用解釋太多。
好奇的同學就問了,蚊子從一開始相對地面靜止是如何加速到83m/s的速度呢?(雖然這個速度很大,但是實際上在加速階段,高鐵的平均加速度只有約0.2m/s2,并不算很大)

在加速階段,如果蚊子是在車廂內(nèi)部固定表面作以停留,摩擦力做功,蚊子跟著高鐵一起加速,也就和高鐵輕松地達到相同的速度,就和坐在列車上的乘客一樣。
猜大家點進來也不是只想看這樣的結論,老師說過“做物理題一定要揣摩出題人的意圖。”大家想知道的肯定是下面的內(nèi)容——車廂內(nèi)懸空的蚊子是如何加速到和高鐵相同速度的?接下來,我們主要從定性的角度出發(fā)來解釋這些問題。
一
車廂內(nèi)懸空的蚊子是如何加速到和高鐵相同速度的?
為了阻止可恨的蚊子和我們保持同樣的速度。假設我們在車廂內(nèi)部的每個角落都抹上了一種超潤滑的物質(zhì),讓蚊子根本不能“搭便車”,否則就要在車廂上來一段地板動作。

此時我們假設蚊子在車廂中,并沒有前后左右運動(杠精先別抬杠),只是懸停在空中,此時豎直方向上的力達到平衡。

豎直方向上,蚊子扇動翅膀提供的升力F升,空氣的浮力F空浮,蚊子所受的重力G三力平衡。
高鐵將會以a的加速度向前運動,要知道蚊子此時是怎么運動的,最關鍵的是進行此時的受力分析。
二
蚊子此時如何受力?
我們知道牛頓運動定律只適用于慣性參考系。比如在日常分析問題時,地球就是一個很好的慣性參考系。現(xiàn)在,高鐵車廂正在相對于地面,做勻加速直線運動。顯然,高鐵不能被視為一個慣性參考系,它是一個典型的非慣性參考系。那么牛頓運動定律是不是在這個參考系中就完全不能適用了嗎?
聰明的科學家想到了一個辦法,就是引入一個虛擬的“慣性力”。大小為ma,方向與加速度相反。雖然這個力是虛擬的,但是在非慣性系之中,引入了慣性力之后,牛頓運動定律就能重新適用了。就比如我們常說的離心力,就是引入的一種“不存在”的慣性力。那么我們看接下來的分析。
因為車廂是非慣性參考系,所以車廂內(nèi)的所有物質(zhì)正在受到一個大小為ma,指向高鐵尾部的慣性力,就好像我們在剛啟動的車上能夠很明顯的感受到背推感一樣,我們在坐電梯的時候也會有同樣失重和超重的感覺。受到的慣性力即為
G‘=m蚊a
在車廂內(nèi)受到慣性力的不只有蚊子,車廂內(nèi)的空氣也受到這種慣性力。所以空氣就擁有了能夠讓其中物體擁有指向高鐵頭部的等效空氣浮力,我們假設空氣此時是不可壓縮的平衡態(tài)的流體,所以我們能夠套用浮力定律來描述這種等效浮力。我們不能再將蚊子當成一個質(zhì)點,我們開始關注它的形狀。
F空浮‘=ρ空aV排
說到這里,這兩種力是否就已經(jīng)平衡了呢?答案是否定的,如果平衡,就會得出m蚊=ρ空V排,即蚊子的密度等于空氣密度,也就是說我們拿一只剛拍死的蚊子,松手之后它就會懸浮在空中,這也太離譜了。

正常情況下蚊子的密度是大于空氣的。所以,從上一節(jié)中我們可以看到,在空氣中蚊子除了受到浮力之外還要提供一定向上的升力,才能懸停在空中。
接下來我們要開車了!
一旦高鐵開動,由于慣性力大于等效浮力。蚊子相對于車廂中的空氣向車廂尾部做加速運動,這就意味著蚊子會受到相反方向即指向高鐵頭部的空氣阻力。
蚊子相對車廂空氣運動速度小,相比于壓差阻力,粘滯阻力占主導,故這里采用斯托克斯定律描述阻力。假設物體是球形的,而且液體相對于球體作層流運動。則阻力大小為,
F阻=6πηυR
其中,R是球體的半徑,υ是它相對于流體的速度,η是流體的粘滯系數(shù)。
因為豎直方向上受力平衡,所以可以只分析水平方向上的受力。所以在以高鐵為參考系時,受力圖如圖。
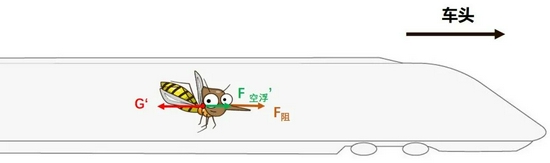
注意此時F阻是隨相對速度增大而增加的,圖中的箭頭長度并不代表實際的大小
三
蚊子此時如何運動?
分析完了受力,我們來分析運動,此時的蚊子其實可以繼續(xù)等效成一個質(zhì)點,它在高鐵的系統(tǒng)中的運動速度會持續(xù)增大,空氣阻力也會逐漸增大,這是一個變加速過程,直到
F空浮‘+F阻=G‘
此時蚊子開始相對車廂勻速向車尾運動。并且這個過渡到穩(wěn)態(tài)的時間預計不會太久,畢竟蚊子在空氣中飛行的阻力是很大的,不信的話可以試試將一只死蚊子向前扔出去,應該落得不會太遠。
其實以上的分析也是很好理解的,這也是為什么,天上下的雨最終是以勻速落在地上的。

雨滴最終下落的速度來源:知乎@芝了
雨滴最終都會達到重力與空氣阻力和空氣浮力的平衡,以勻速落下。
我們可以合理估算一下,蚊子在這種情況下相對車廂最多有多大的收尾速度大致有多少。由前文可知高鐵加速度為0.2m/s2,蚊子重量一般約為2mg,蚊子的大小為毫米量級,取15℃時,空氣粘度為1.81×10-5 kg/(m·s)。
我們大致合理估算了一下,收尾速度大約在cm/s的數(shù)量級(防杠補丁:由于時間倉促,小編只算了一遍,如果大家有興趣驗算的話,和該結果差太多,歡迎在評論區(qū)補充)。照這個速度運動下去,蚊子就算碰在車上也沒有任何事。
四
一些奇葩的腦洞
老師也說過“做題要學會舉一反三”。
現(xiàn)在我們假設車廂里面空氣都被抽走了,會發(fā)生什么事情呢?于是上面提到的和空氣有關的力都消失了,包括蚊子本身扇動翅膀的升力。所以還沒等高鐵開動,蚊子就吧唧一下掉地上滑走了。

大家再思考一個問題,什么情況下蚊子會因為高鐵的運動而相對高鐵向前運動呢?
首先考慮一個和剛剛相反的情況,高鐵是在減速運行,那么按照剛才的結論,蚊子就會相對車廂向前運動。
再進一步,如果不是蚊子而是其它的物體呢?
給大家一個高中的物理題作為線索。
運輸液體的槽車,液體上面有氣泡,如圖,當車向前開動時,氣泡將向什么方向運動。

是的,只要懸浮的物體足夠輕,它的密度小于空氣的密度,就可以使等效浮力大于慣性力。它就可以向車頭移動。
如果高鐵的前后都是敞篷的 ,也就是說高鐵里的空氣是留不住的,又會發(fā)生什么呢?這時,因為加速帶來的等效的浮力也就消失了,所以蚊子在高鐵向前加速時并不會受到空氣對它向前的空氣阻力,只會呆呆的停留在原地。高鐵開走后,蚊子呆呆的望著身下的鐵軌,發(fā)出了靈魂的質(zhì)問?
如果我們讓模型再完善一些,賦予車廂內(nèi)的蚊子一定的主觀能動性。蚊子現(xiàn)在可以上下左右前后地任意飛了。那么蚊子怎么跟上高鐵的速度呢?
就是單純飛啊!!還管什么受力分析?

說到最后,一切剛剛做的模型和受力在真實的蚊子身上都是那么的不值一提。真實情況下,蚊子想怎么飛就怎么飛,根本沒有任何為蚊子操心的必要。
那我們用物理去解釋又有什么意義?
我們并不是看到運動就想建模,并不是看到受力就想分析,也并不是看到假科普就想去錘(其實也是)。只是希望能夠讓物理的理性,融入進大家日常的生活中。
物理建模就是在現(xiàn)象中抽象出最本質(zhì)的特征,可能剛建立的模型足夠簡單,并不能解決實際問題,但是對于我們領悟事情背后的本質(zhì)是重要的。
來源:中科院物理所

“掌”握科技鮮聞 (微信搜索techsina或掃描左側二維碼關注)

















