新浪科技訊 北京時間5月10日消息，據國外媒體報道，關于宇宙，我們可以提出許多無比宏大的問題。這些問題直擊“現實究竟是什么”的核心，在歷史上曾引發無數人苦思冥想。例如，“宇宙是什么？”、“宇宙有多大？”、“宇宙是永恒存在的、還是突然出現的呢？如果是后一種情況，那它是何時出現的？”這些都曾是最令人費解的哲學問題，但就在過去100年間，我們已經找到了確切、科學的答案。我們已經知道了宇宙是什么，知道了可觀測宇宙的直徑約為920億光年，也知道了我們所知的宇宙開始于138億年前，并且以上數值的不確定性只有1%左右。

　　但無論是對時間還是距離的衡量，我們使用的都是以地球為中心的單位，比如“年”和“光年”。有沒有一種更加客觀、更加通用的衡量方式呢？答案當然是“有”。就像天文學家杰瑞·貝爾所寫的那樣：

　　“為何對宇宙的計算全都要用到‘年’這個單位呢？在我看來，‘年’是個很狹義的概念。畢竟，‘年’存在的基礎（即恒星）出現至今也不過幾十億年，僅占宇宙當前年齡的三分之一。就連‘光年’這個關鍵概念也要與這種狹義的測量單位捆綁在一起。”

　　這幾點都說得很好，值得我們在此基礎上進行延伸和思考、尋找替代方案。首先，我們要了解測量宇宙時間背后涉及到哪些科學原理。

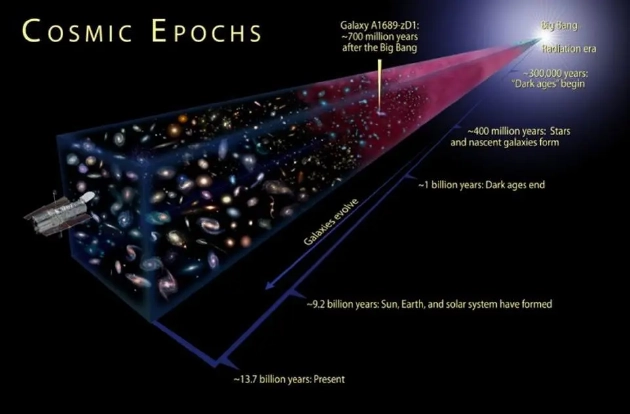　　雖然我們可以觀察到成千上萬光年、甚至數億光年之外的宇宙，但以地球上的“年”來計算宇宙年齡、以“光年”衡量宇宙距離仍是一種“地心說”的思維。這真的是我們唯一的、甚至最佳的選擇嗎？

　　在地球上，要想理解時間流逝的概念、并利用重復出現的規律現象開展生物活動，其實只有兩種方法。在較短的時間尺度上，我們有“天”的概念。而這一概念很重要，因為一天代表著日出和日落，大致對應一次完整的地球自轉，還與大多數動植物的活動與休眠周期保持一致。這些現象都會日復一日地循環往復下去。

　　但一旦將時間尺度拉長，就能看出每一天之間的區別了。例如，在一年的時間里，日出和日落的時間會逐漸提前或推遲，白天的時長會逐漸增加或減少，太陽高度會漸漸升高或降低，四季會循環變遷，動植物和其它生物的活動也會隨之改變。而這些現象又會在接下來的每一年里循環往復，幾乎不會有任何變化。

　　這樣看來，不難理解我們為何會提出圍繞“天”和“年”等概念的計時體系，因為我們在地球上的生活與這些周期性現象密不可分。然而，我們在地球上經歷的“天”和“年”并不能很好地對應宇宙中時間的流逝，原因有很多。

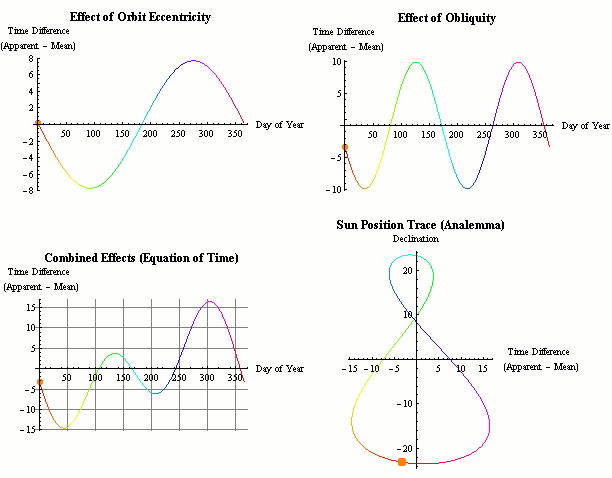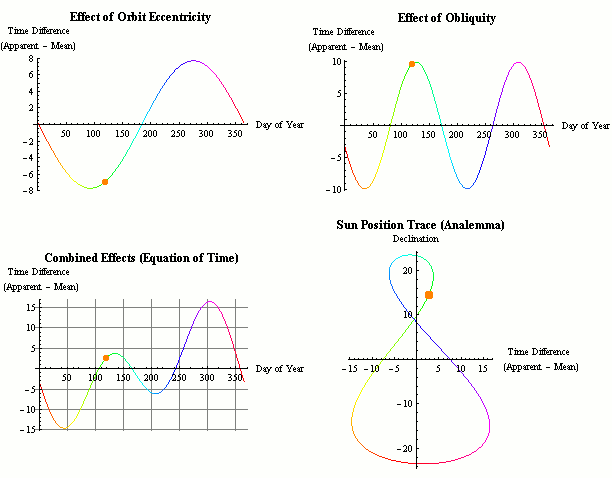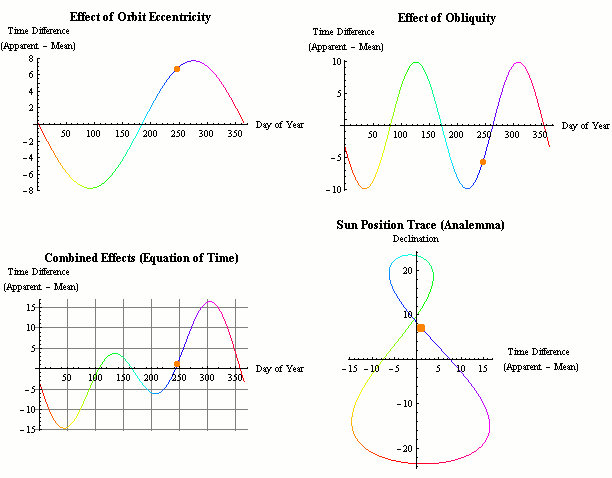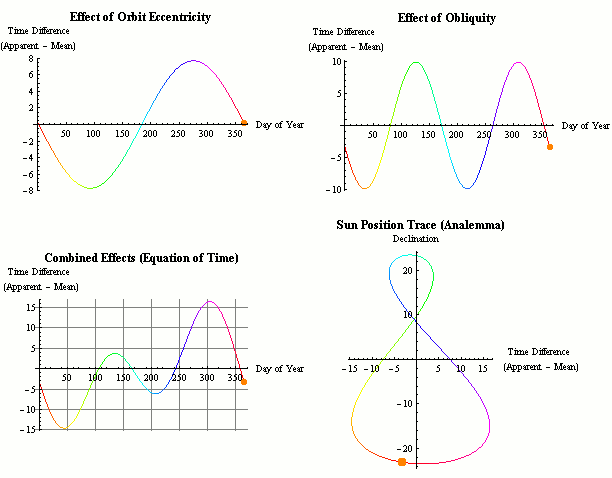　　由于地球圍繞太陽運動的軌道為橢圓形，地球在近日點時速度會加快，在遠日點時速度會減慢，因此日出和日落的時間會不斷變化，白天的長度也會不停增減。這些規律會以年為單位重復發生。

　　首先，一天的長度在地球歷史上已經發生了顯著改變。在月球、地球和太陽之間的相互作用下，潮汐摩擦力導致每天變得越來越長，月球也離地球越來越遠。大約40億年前，地球上的“一天”只有6至8小時，一年對應的時長超過1000天。

　　不過，在太陽系歷史中，“年”的變化倒并不大。一年代表著地球圍繞太陽完整旋轉一周所需的時間。其中最大的影響因素為太陽的質量。到目前為止，太陽已經減少了相當于一整顆土星的質量，導致地球到太陽的距離稍微變遠了一些，并且公轉速度也略有減緩，因此“一年”的長度有所增加，不過增加的幅度很小，僅為萬分之二。相當于從太陽系誕生之初到現在，每年的時長增加了兩小時左右。

　　即使太陽系中有如此多復雜的天體物理學現象，一年的時長卻幾乎沒有變化，因此對我們來說，“年”就是用于大尺度計時最為穩定的基準。由于光速是一個已知、且可測量的常數，“光年”作為一個距離單位，便自然而然地衍生了出來。隨著時間的流逝，光年的變化也是微乎其微，數十億年間的變化幅度僅為0.02%。

　　地球軌道并不是正圓形，而是橢圓形。軌道的長軸與短軸比會不斷改變。而地球轉動一圈的時間決定了一年的長度，所以年的長度也會緩慢變化。

　　此外還有一個重要單位，不過它是在“年”的基礎上間接定義而來的，也就是“秒差距”。它不僅以時間為基礎，還以天文學角度和三角學為基礎。在地球圍繞太陽旋轉過程中，即使是原地不動的恒星之間的相對位置也會發生變化，就像你的兩只眼睛交替睜眼時看到的情況一樣，離你更近的物體相對于遠處背景物的位置似乎有所改變。

　　在天文學中，我們將這種現象稱為“視差”，用來作為參照的長度也不是兩眼之間的距離，而是地球相對于太陽的最大位置差，即地球軌道半徑，約等于3億公里。當一個天體相對于遙遠背景中天體的運動角度為1角秒時，兩者之間的距離便被定義為1秒差距，約等于3.26光年。

　　但我們憑什么將自己對時間的定義強行推廣到整個宇宙中呢？這種做法很不客觀，仍未脫離“地心說”思維的桎梏。無論是天還是年，都不應作為整個宇宙的時間測量單位；同理，無論是光年還是秒差距（還有相關的千秒差距、百萬秒差距等等），也都不應作為整個宇宙的距離測量單位。

　　事實上，我們已經找到了一些更加客觀、更加遵從物理學的時間定義方式。它們雖不存在“地心說”帶來的種種缺陷，但也有自己的問題。你可以思考一下，自己是更喜歡這些方法、還是更喜歡目前以年為基礎（也是以地球為基礎）的計時方法。

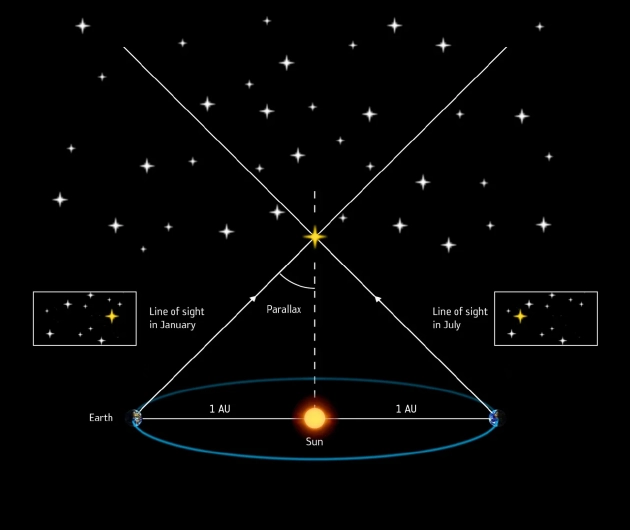　　在地球圍繞太陽旋轉過程中，地球附近的恒星相對于遙遠恒星的位置似乎會發生周期性變化。當一顆恒星的視角為1角秒（即1度角的3600分之一）時，其到地日系統的距離就剛好為1秒差距，約為3.26光年。

　　1）普朗克時間

　　有沒有一種對時間的定義完全以宇宙基本常數為基礎呢？答案就是“普朗克時間”。宇宙中有三大可測量的基本常數：萬有引力常數G、光速c、以及量子常數h（例如約化普朗克常數）。將它們結合起來，便可創造出一個基本時間單位：（G×h÷c5）的平方根，結果為5.4×10-43，宇宙中的任何觀察者都能得出同樣的結論。

　　不過，這個時間單位只適用于極小尺度。在此尺度上，物理法則統統都會失效，因為該尺度上的量子波動不會形成粒子/反粒子對，而是會形成黑洞，沒有任何物理過程能與如此小的時間尺度相匹配。要想運用普朗克單位來描述時間，哪怕只是亞原子級的物理過程，也會是個天文數字。例如，目前已知壽命最短的亞原子粒子是丁夸克，其衰變時長約為1018個普朗克時間，而傳統意義上的“一年”則會超過1051個普朗克時間。所以這種計時方式本身沒什么問題，就是使用起來太不方便了。

　　2）原子鐘

　　這張藝術家繪制的概念圖描繪了時空的泡沫狀結構，其中細小的泡泡只有原子核的十萬億分之一大。它們會不斷波動、并且轉瞬即逝。但它們的體積是存在下限的，一旦小于這一下限，物理學就無法再發揮作用。這個下限叫做普朗克尺度，在距離上相當于10-35米，時間相當于10-43秒。

　　一個有趣的事實是，所有對時間、質量和距離的定義都完全是由人類自己決定的，一秒、一克、或一米其實沒有任何意義，我們只是選擇將這些數值作為日常生活中的標準而已。但我們可以將這些量相互聯系起來，就像剛才用三大基本常數定義普朗克時間一樣。

　　既然如此，我們能否用原子躍遷（即電子從較高能級降到較低能級、同時釋放出特定頻率和波長的光線）來定義時間和距離呢？頻率是時間的倒數，因此可以將 “時間”定義為光線傳播一個波長所需的時長，將“距離”定義為一個波長的長度。這就是原子鐘的作用機制，也是我們對秒和米定義的基礎。

　　但這種定義依然很專斷，而且大多數躍遷發生的速度都很快，時間間隔極短，不適合日常使用。例如，秒的現代定義是銫-133原子的超精細結構釋放出的光子在真空中傳播9，192，631，770個波長所需的時間。那么年和光年呢？用這種計時方法，得出的依然是一堆天文數字，對大多數人來說都實在太麻煩了。

　　3）哈勃時間

　　兩臺原子鐘的高度哪怕僅相差33厘米，鐘表運行的速度也會發生顯著差異。這讓我們不僅可以測得引力場的強度，還能測得其梯度變化，因此可用于測量海拔/標高。原子鐘以原子中的電子躍遷為基礎，是人類目前最精確的計時工具。

　　接下來讓我們走向另一個極端，從量子世界直接上升到宇宙尺度。宇宙正以一定速率不斷膨脹，這個膨脹率一般被稱作哈勃參數、又稱哈勃常數。雖然我們一般將其寫成“速度/距離”的形式，比如“71 km/s/Mpc”（即71公里/秒/百萬秒差距），它也可以簡單地寫成時間的倒數，即2.3×10-18s-1，再將其倒過來，我們就得到了1個單位的“哈勃時間”，即4.3×1017秒，大致等于宇宙自大爆炸發生以來的年齡。

　　再將這一時間乘以光速，就得到了“哈勃距離”，約為1.3×1013米、或者137億光年，約等于從地球到宇宙邊緣距離的30%。

　　這樣一番演算下來，結果似乎很理想，得出的距離尺度和時間尺度都可以與真正的宇宙規模相匹配了。但問題在于，哈勃常數并不是真正的“常數”，隨著宇宙的年齡不斷增加，這個數值會不斷減小，而且背后的機制很復雜（取決于宇宙不同組成部分的相對能量密度）。所以這種計時理念雖然很有意思，但并不現實，因為對宇宙中的不同觀察者而言，宇宙自大爆炸以來經歷的時間都不盡相同，哈勃距離和哈勃時間也要做相應的調整。

　　4）氫原子自旋

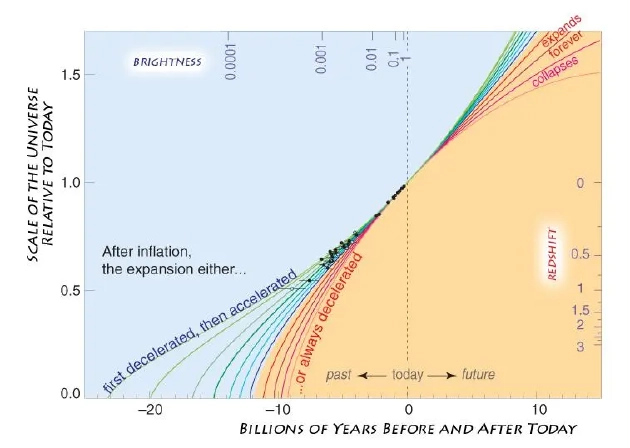　　測量過去的時間和距離可以幫助我們預測宇宙未來的演化方向。將膨脹率與宇宙中的物質和能量聯系在一起，便可得出宇宙的“哈勃時間”，但哈勃時間并不是常數，而是會隨著宇宙的膨脹和時間的流逝發生改變。

　　到目前為止，我們的每次嘗試似乎都不太適用于宇宙尺度，但不要沮喪，還有一種可能性值得思考。中性的氫原子由一個電子和一個原子核結合而成，原子核中一般只有孤零零的一個質子。當電子達到基態時，其相對于質子可能有兩種配置方式。要么電子和質子的量子自旋方向相反，即分別為+?和-?；要么方向相同，即均為+?或均為-?。

　　若自旋方向相反，此時電子的確處于最低能態；但若自旋方向相同，那么電子的旋轉方向有一定概率會發生翻轉，釋放出一個頻率為1，420，405，751.77 Hz的光子。通過換算，這個頻率對應的時間為0.7納秒，長度約合21厘米。

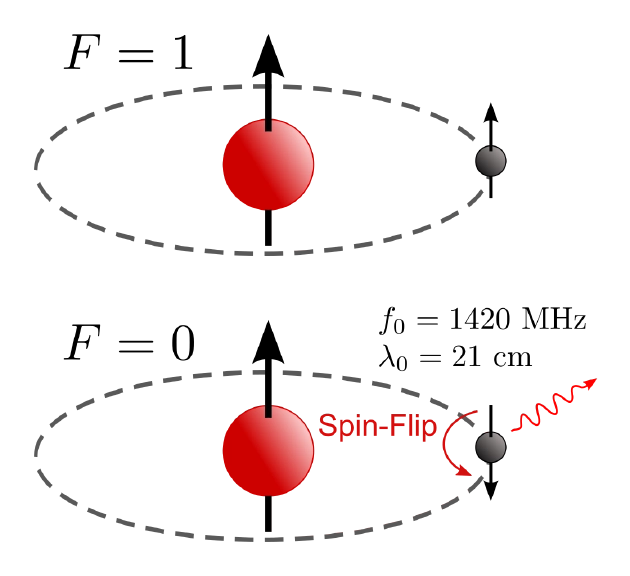　　當一個氫原子形成時，其中電子和質子的自旋方向有50%的可能性相同、50%的可能性相反。如果相反，電子就不會再發生躍遷。如果相同，電子就可能躍遷到更低的能態上，釋放出一個特定波長的光子，這一過程的時間尺度相當長。

　　最有意思之處在于，這個躍遷速度在天文學層面上其實是比較緩慢的，相當于2.9×10-15s-1。轉化為宇宙時間和宇宙長度，分別得到1090萬年和1090光年，約等于3.3百萬秒差距。在我們已知的所有自然界基本常數中，這是最容易轉化為宇宙級時間尺度和距離尺度的一個。

　　但最最重要的是，我們選擇的時間定義無論如何都是專斷的。在涉及時長或距離的問題上，不同的定義對我們得出的答案其實并沒有什么影響。只要我們定義的時間間隔維持不變，這些答案在本質上就都是相同的。

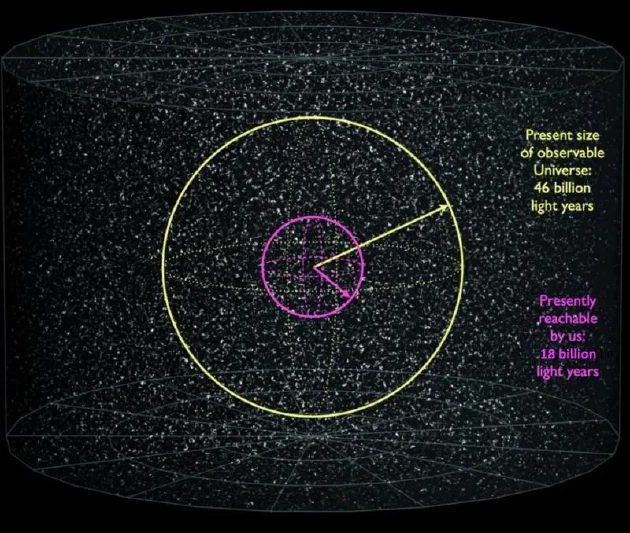　　圖為我們可以觀測的宇宙范圍（黃圈）和可以到達的宇宙范圍（紫紅色）。可見宇宙半徑為461億光年，假如在過去138億年間，有一個發光物體隨著宇宙膨脹一直在遠離地球，其發出的光線要想在今天剛好抵達地球，這一半徑就是該物體與地球距離的上限。但就算我們能以光速飛行，我們也永遠到不了180億光年以外的星系。無論將上述距離和時間轉化成什么單位，得出的結論都是相同的。

　　那么，不同的時間定義方式之間究竟有什么區別呢？歸根到底，區別其實在于我們身為人類、理解這些定義和數字的能力。在閱讀天文學文獻時，你會看到以年描述的時間，還會看到以天文單位、秒差距、千秒差距、百萬秒差距、甚至十億秒差距描述的距離，具體取決于描述的對象是太陽系、恒星間、星系內、星系間、還是宇宙級距離。但由于我們是人類，我們在直覺上能夠很好地理解“年”的概念，只要用年乘以光速，便可進一步得出光年的概念。這雖然不是唯一選項，卻是目前為止最常用的做法。也許在目不可及的未來，人類將脫離地球的束縛、飛向遙遠的外太空，到那時，我們使用的單位也將脫離“地心說”的桎梏。（葉子）