新浪科技訊 北京時(shí)間12月28日消息，據(jù)國(guó)外媒體報(bào)道，數(shù)學(xué)是一門研究數(shù)量、結(jié)構(gòu)、變化和空間等概念的學(xué)科，一些開創(chuàng)性的數(shù)學(xué)概念不僅改變了人類的歷史，也深刻改變了我們所處的這個(gè)世界。

　　數(shù)學(xué)方程是我們了解世界的獨(dú)特窗口，它們讓現(xiàn)實(shí)變得有意義，幫助我們看到了以往未曾注意到的東西。因此，數(shù)學(xué)上的新進(jìn)展往往伴隨著我們對(duì)宇宙的理解進(jìn)一步加深。接下來(lái)，就讓我們來(lái)了解一下歷史上著名的9個(gè)方程，從微小的粒子到浩瀚的宇宙，它們徹底改變了人類看待世間萬(wàn)物的方式。

　　勾股定理

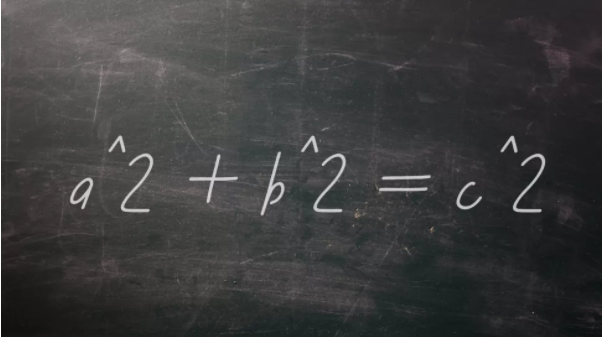
　　人們?cè)趯W(xué)校里學(xué)到的第一個(gè)重要的三角函數(shù)就是直角三角形邊長(zhǎng)之間的關(guān)系：兩條直角邊（較短的直角邊古稱勾長(zhǎng)，較長(zhǎng)的直角邊古稱股長(zhǎng)）的長(zhǎng)度的平方和等于斜邊長(zhǎng)（古稱弦長(zhǎng)）的平方。這條定理通常被寫為：a^2 + b^2 = c^2。從古巴比倫時(shí)代起，該定理至少已存在了3700年。

　　勾股定理是人類早期發(fā)現(xiàn)并證明的重要數(shù)學(xué)定理之一。英國(guó)蘇格蘭圣安德魯斯大學(xué)的研究者認(rèn)為，古希臘數(shù)學(xué)家畢達(dá)哥拉斯寫下了該定理今天被廣泛使用的方程形式，現(xiàn)代西方數(shù)學(xué)界也因此稱其為“畢達(dá)哥拉斯定理”。除了在建筑、導(dǎo)航、制圖和其他重要過程中有所應(yīng)用外，勾股定理還幫助擴(kuò)展了數(shù)字的概念。公元前5世紀(jì)，梅塔龐通（Metapontum）的數(shù)學(xué)家希帕索斯注意到，如果一個(gè)等腰直角三角形兩條腰長(zhǎng)度為1，則其底邊長(zhǎng)便是根號(hào)2（），這是一個(gè)無(wú)理數(shù)（在此之前的歷史中，還沒有人見過這樣的數(shù)）。根據(jù)劍橋大學(xué)的一篇文章，希帕索斯據(jù)說是被扔進(jìn)海里的，因?yàn)楫呥_(dá)哥拉斯的追隨者（包括希帕索斯）對(duì)所謂的“無(wú)限不循環(huán)小數(shù)”感到非常震驚和恐慌。當(dāng)時(shí)的畢達(dá)哥拉斯學(xué)派認(rèn)為“萬(wàn)物皆數(shù)”，世界上只有整數(shù)和分?jǐn)?shù)（有理數(shù)），希帕索斯的發(fā)現(xiàn)引發(fā)了第一次數(shù)學(xué)危機(jī)。

　　F = ma和萬(wàn)有引力定律

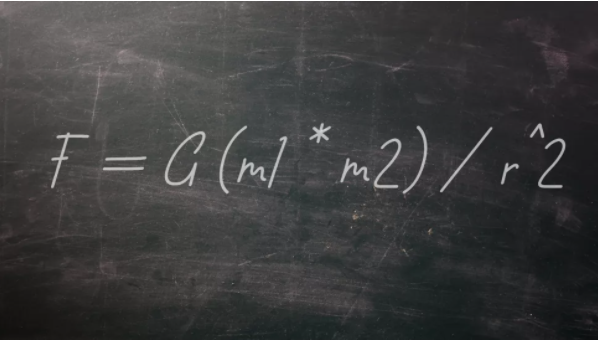
　　艾薩克·牛頓是英國(guó)乃至人類科學(xué)史上最杰出的人物之一，提出了大量改變世界的發(fā)現(xiàn)，其中就包括牛頓第二運(yùn)動(dòng)定律。該定律指出，力等于物體的質(zhì)量乘以加速度，通常寫作F = ma。通過對(duì)這一定律的擴(kuò)展，結(jié)合其他實(shí)驗(yàn)觀測(cè)結(jié)果，使牛頓在1687年描述了我們今天所謂的萬(wàn)有引力定律：F = G （m1 * m2） / r^2，其中F是兩個(gè)物體之間的萬(wàn)有引力，m1和m2是兩個(gè)物體的質(zhì)量，r是它們之間的距離；G是一個(gè)基本常數(shù)，稱為萬(wàn)有引力常數(shù)，它的值必須通過實(shí)驗(yàn)測(cè)量。據(jù)記載，卡文迪許第一個(gè)在實(shí)驗(yàn)室內(nèi)完成了測(cè)量?jī)蓚€(gè)物體之間萬(wàn)有引力的實(shí)驗(yàn)，準(zhǔn)確求出了萬(wàn)有引力常數(shù)和地球質(zhì)量，其他人則借助他的實(shí)驗(yàn)結(jié)果求得了地球密度。

　　牛頓第二定律被譽(yù)為經(jīng)典力學(xué)的靈魂，能夠主導(dǎo)各種物體運(yùn)動(dòng)和物理現(xiàn)象，其用途也非常廣泛。牛頓運(yùn)動(dòng)定律的許多概念也被用于理解各種復(fù)雜的物理系統(tǒng)，包括太陽(yáng)系中行星的運(yùn)動(dòng)，以及如何使用火箭在它們之間旅行。

　　波動(dòng)方程

　　利用牛頓提出的運(yùn)動(dòng)定律，18世紀(jì)的科學(xué)家們開始分析他們周圍的一切。據(jù)2020年發(fā)表在《歷史研究進(jìn)展》（Advances in Historical Studies）雜志上的一篇論文介紹，博學(xué)多才的法國(guó)物理學(xué)家、數(shù)學(xué)家和天文學(xué)家讓·勒朗·達(dá)朗貝爾在1743年推導(dǎo)出了一個(gè)描述弦振動(dòng)或波動(dòng)現(xiàn)象的方程。該方程可以寫作：

　　1/v^2 * ?^2y/?t^2= ?^2y/?x^2

　　在這個(gè)方程中，v是波的速度，其他部分描述的是波在一個(gè)方向上的位移。利用擴(kuò)展到二維或多維的波動(dòng)方程，研究人員得以預(yù)測(cè)水、地震波和聲波的運(yùn)動(dòng)。該方程也是量子物理學(xué)中薛定諤方程的基礎(chǔ)，后者使許多現(xiàn)代計(jì)算機(jī)設(shè)備成為可能。

　　傅里葉方程

　　無(wú)論你有沒有聽說過法國(guó)數(shù)學(xué)家、物理學(xué)家讓-巴蒂斯特·約瑟夫·傅里葉男爵，他的工作都早已影響了你的生活。他在1822年寫下的數(shù)學(xué)方程使研究人員能將復(fù)雜、混亂的數(shù)據(jù)分解成簡(jiǎn)單波的組合，從而更容易分析。根據(jù)《耶魯科學(xué)》（Yale Scientific）雜志上的一篇文章，傅里葉變換的基本思想在提出時(shí)是一個(gè)激進(jìn)的概念，許多科學(xué)家拒絕相信復(fù)雜的系統(tǒng)可以簡(jiǎn)化到如此優(yōu)雅的程度。然而，在今天的許多現(xiàn)代科學(xué)領(lǐng)域，包括數(shù)據(jù)處理、圖像分析、光學(xué)、通信、天文、工程、金融、密碼學(xué)、海洋學(xué)和量子力學(xué)等領(lǐng)域中，傅里葉變換有著廣泛的應(yīng)用。例如在訊號(hào)處理中，傅里葉變換的典型用途就是將訊號(hào)分解為振幅分量和頻率分量。

　　麥克斯韋方程組

　　電和磁在19世紀(jì)還是全新的概念，當(dāng)時(shí)的學(xué)者們都在研究如何捕捉并利用這些奇怪的物理現(xiàn)象。1864年，蘇格蘭數(shù)學(xué)家和物理學(xué)家詹姆斯·克拉克·麥克斯韋發(fā)表了一個(gè)包含20個(gè)方程的方程組，描述了電場(chǎng)和磁場(chǎng)如何產(chǎn)生作用，以及它們之間的相互關(guān)系。該方程組極大地促進(jìn)了我們對(duì)這兩種現(xiàn)象的理解。現(xiàn)在，麥克斯韋方程組由四個(gè)一階線性偏微分方程組成，分別是描述電荷如何產(chǎn)生電場(chǎng)的高斯定律、表明磁單極子不存在的高斯磁定律、解釋時(shí)變磁場(chǎng)如何產(chǎn)生電場(chǎng)的法拉第感應(yīng)定律，以及說明電流和時(shí)變電場(chǎng)如何產(chǎn)生磁場(chǎng)的麥克斯韋-安培定律。這個(gè)方程組是所有大學(xué)一年級(jí)的物理系學(xué)生都要學(xué)習(xí)的內(nèi)容，也為現(xiàn)代科技世界中所有的電子方程奠定了基礎(chǔ)。

　　E = mc ^ 2

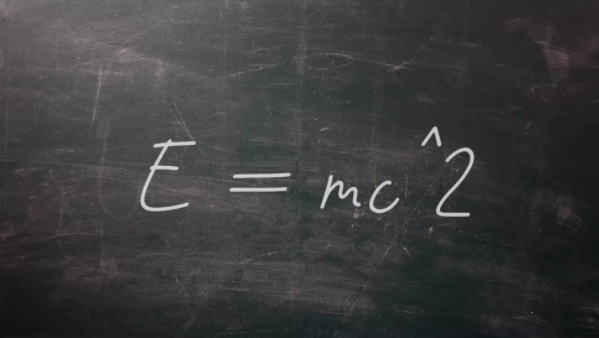
　　如果沒有這個(gè)著名的方程，任何一個(gè)變換方程列表都不可能是完整的。1905年，阿爾伯特·愛因斯坦首次提出了質(zhì)能等價(jià)的概念，即E = mc^2，這是他開創(chuàng)性的狹義相對(duì)論的一部分。E = mc^2表明，物質(zhì)和能量是同一個(gè)事物的兩面，方程中E代表能量，m代表質(zhì)量，c代表恒定的光速。如此簡(jiǎn)單的方程中所包含的概念，至今仍讓許多人難以理解，但如果沒有E = mc ^ 2，我們就無(wú)法理解宇宙中恒星的存在，也不知道如何建造像大型強(qiáng)子對(duì)撞機(jī)這樣的巨型粒子加速器，更無(wú)法一窺亞原子世界的本質(zhì)。可以說，這個(gè)方程已經(jīng)成為人類歷史上最著名的方程之一，并成為了文化的一部分。

　　弗里德曼方程

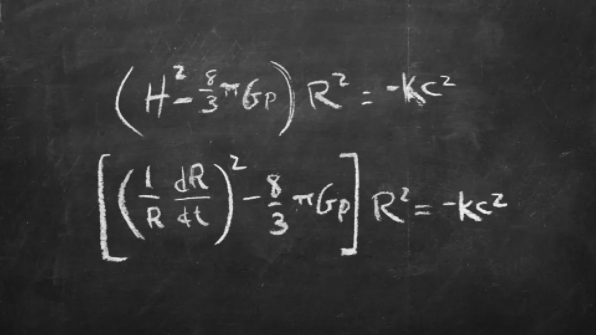
　　用一組方程來(lái)定義整個(gè)宇宙，聽起來(lái)似乎是一個(gè)狂妄自大的想法，但這正是俄羅斯物理學(xué)家亞歷山大·弗里德曼在20世紀(jì)20年代所提出的重要思想。利用愛因斯坦的相對(duì)論，弗里德曼指出，從大爆炸開始，膨脹宇宙的特征可以用兩個(gè)獨(dú)立的方程來(lái)表示。

　　這兩個(gè)方程把宇宙的所有重要參數(shù)，包括宇宙的曲率、宇宙包含多少物質(zhì)和能量、宇宙擴(kuò)張的速度，與一些重要的常數(shù)，如光速、重力常數(shù)和哈勃常數(shù)等結(jié)合起來(lái)。這是一個(gè)在廣義相對(duì)論框架下，描述空間上均一且各向同性的膨脹宇宙模型。眾所周知，愛因斯坦并不喜歡宇宙膨脹或收縮的觀點(diǎn)，他的廣義相對(duì)論認(rèn)為，這些情況的發(fā)生是收到了引力的影響。愛因斯坦試圖將一個(gè)標(biāo)為“λ”變量添加到愛因斯坦方程中，作為宇宙學(xué)常數(shù)，使方程能有靜態(tài)宇宙的解。在哈勃提出膨脹宇宙的觀測(cè)結(jié)果——哈勃紅移——之后，愛因斯坦放棄了宇宙學(xué)常數(shù)，并認(rèn)為這是他“一生中最大的錯(cuò)誤”。不過，幾十年后，這一概念又被重新拾起。研究者認(rèn)為宇宙學(xué)常數(shù)盡管值很小，但可能不為0；而且該常數(shù)可能以暗能量的形式存在，而暗能量推動(dòng)著宇宙的加速膨脹。

　　香農(nóng)信息方程

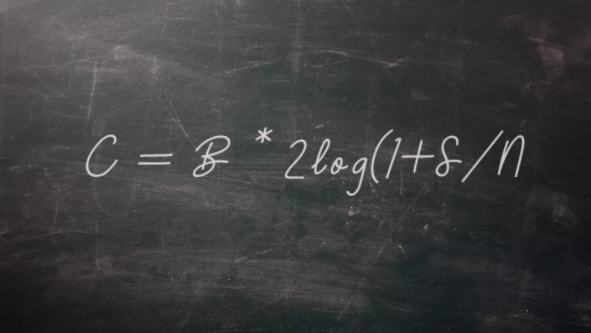
　　大多數(shù)人都熟悉構(gòu)成計(jì)算機(jī)二進(jìn)制數(shù)字的0和1。但是，如果沒有美國(guó)數(shù)學(xué)家和工程師克勞德·香農(nóng)的開創(chuàng)性工作，這一關(guān)鍵概念就不會(huì)發(fā)展起來(lái)。在1948年一篇的重要論文中，香農(nóng)提出了一個(gè)方程，用來(lái)表明信息傳輸?shù)淖畲笮剩ǔ懽鳎篊 = B * 2log（1+S/N）。式中，C為特定通信通道可達(dá)到的最高無(wú)錯(cuò)誤數(shù)據(jù)速度，B為通道帶寬，S為平均信號(hào)功率，N為平均噪聲功率（S / N表示系統(tǒng)的信噪比）。這個(gè)方程的輸出以每秒比特?cái)?shù)（bps）為單位。在1948年的論文中，香農(nóng)將比特（bit）作為“二進(jìn)制數(shù)字”（binary digit）的縮寫，并將其概念歸功于數(shù)學(xué)家約翰·W·圖基。

　　羅伯特·梅的單峰映象

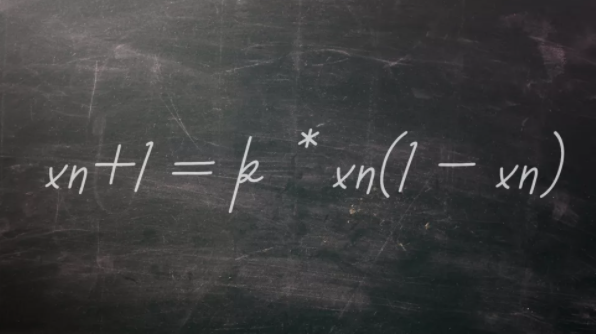
　　非常簡(jiǎn)單的事情有時(shí)會(huì)產(chǎn)生難以想象的復(fù)雜結(jié)果。這個(gè)不言自明的道理看起來(lái)似乎并不怎么激進(jìn)，但直到20世紀(jì)中期，科學(xué)家們才完全理解了這個(gè)概念的重要性。當(dāng)時(shí)，混沌理論領(lǐng)域剛剛崛起，研究人員發(fā)現(xiàn)，只具有少數(shù)部分反饋的系統(tǒng)可能會(huì)產(chǎn)生隨機(jī)和不可預(yù)測(cè)的行為。1976年，澳大利亞物理學(xué)家、數(shù)學(xué)家、生態(tài)學(xué)家羅伯特·梅在《自然》（Nature）雜志上發(fā)表了一篇題為《簡(jiǎn)單的數(shù)學(xué)模型與非常復(fù)雜的動(dòng)力學(xué)》（Simple mathematical models with very complicated dynamics）的論文，提出了單峰映象（logistic map），在數(shù)學(xué)上可寫作：xn+1 = k * xn（1 - xn）。這是一個(gè)由簡(jiǎn)單非線性方程產(chǎn)生混沌現(xiàn)象的經(jīng)典范例。

　　Xn表示當(dāng)前系統(tǒng)中的某個(gè)量，它通過（1 - Xn）所描述的部分對(duì)自身進(jìn)行反饋。K是常數(shù)，xn+1表示下一時(shí)刻的系統(tǒng)。盡管該方程看起來(lái)很簡(jiǎn)單，但不同的k值會(huì)產(chǎn)生非常不同的結(jié)果，包括一些復(fù)雜和混亂的行為。羅伯特·梅的單峰映象被用于解釋生態(tài)系統(tǒng)中的種群動(dòng)態(tài)，還能為計(jì)算機(jī)編程生成隨機(jī)數(shù)。（任天）