來源： 普林小虎隊

　　編者按

　　2021年10月1日是楊振寧先生的百歲華誕。（楊先生實際年齡99歲，虛歲一百，官方文件上的生日是9月22日。）我們特發(fā)表此文，為楊先生賀。

　　撰文|倪憶

　　楊振寧先生（1922.10.1— ）從來不認(rèn)為自己是一位數(shù)學(xué)家。事實上，楊先生曾經(jīng)說過：“現(xiàn)今只有兩類數(shù)學(xué)著作。一類是你看完了第一頁就不想看下去了， 另一類是你看完了第一句話就不想看下去了。”然而，楊振寧先生對現(xiàn)代數(shù)學(xué)有著廣泛而深遠(yuǎn)的影響。在20世紀(jì)后半葉的物理學(xué)家里，恐怕只有威騰（Edward Witten，1951— ）對數(shù)學(xué)的影響能夠跟楊先生相提并論。本文試圖對楊先生的數(shù)學(xué)貢獻(xiàn)作一些簡單介紹。需要說明的是，這里涉及到許多非常深刻的數(shù)學(xué)，作者本人了解的僅僅是其中一小部分，錯漏之處在所難免，希望方家指正。

　　楊-米爾斯理論

　　楊振寧先生最重要的成果是楊-米爾斯理論（Yang-Mills theory），這是一種非阿貝爾規(guī)范場論（nonabelian gauge theory）。規(guī)范場論的思想在麥克斯韋（James Maxwell，1831—1879）的電磁學(xué)理論里便已經(jīng)出現(xiàn)。1918年，外爾（Hermann Weyl，1885—1955）試圖統(tǒng)一電磁場和引力場，在場論中引入了一個尺度因子。這個尺度因子帶來了一定的冗余度，需要選定一個“規(guī)范”（gauge）來剔除此冗余度。外爾的這一嘗試并未成功，愛因斯坦（Albert Einstein，1879—1955）高度評價其中的數(shù)學(xué)，卻強(qiáng)烈批評其中的物理。[1]

　　普林斯頓高等研究院在四十年代的一次會議，其中有愛因斯坦（左三）和外爾（右二）（圖源：高等研究院檔案）

　　外爾最初引入的尺度因子是正實數(shù)。量子力學(xué)興起后，外爾在1929年修改了他的規(guī)范場論，把尺度因子改成模長為1的復(fù)數(shù)，用以描述電磁場。福克（Vladimir Fock，1898—1974）和倫敦（Fritz London，1900—1954）等人也在這一時期作出了類似發(fā)現(xiàn)。1941年，泡利（Wolfgang Pauli，1900—1958）把規(guī)范場理論普及給物理學(xué)界。

　　在數(shù)學(xué)里，所有模長為1的復(fù)數(shù)組成一個群U（1）。這個群被稱作外爾規(guī)范場論里的規(guī)范群。如果一個群里的乘法是可交換的，這個群就被被稱作阿貝爾群，反之就是非阿貝爾群。例如大多數(shù)矩陣群都是非阿貝爾群，因為乘法交換律對于矩陣乘法不成立。外爾理論里的規(guī)范群是阿貝爾群，所以外爾理論是一個阿貝爾規(guī)范場論。

　　我們知道，自然界中有四種基本力：電磁力、弱相互作用、強(qiáng)相互作用、萬有引力。外爾等人的工作把電磁力用U（1）規(guī)范場論來描述，而萬有引力的物理理論則是愛因斯坦的廣義相對論。1954年，楊振寧和米爾斯（Robert Mills，1927—1999）把規(guī)范場論里的規(guī)范群從U（1）改成二階正交酉矩陣群SU（2），建立了第一個非阿貝爾規(guī)范場論。楊振寧和米爾斯最初想用這一理論來描述強(qiáng)相互作用，但這并不正確。經(jīng)過后來許多物理學(xué)家的努力，SU（2）規(guī)范場論被成功地用于描述弱相互作用。而強(qiáng)相互作用則需要使用規(guī)范群為SU（3）的規(guī)范場論，通常也被稱為楊-米爾斯理論。

　　1999年，楊振寧與米爾斯在楊振寧退休慶祝會議上（圖源：American Institute of Physics）

　　統(tǒng)計學(xué)家斯蒂格勒（Stephen Stigler，1941— ）曾提出一個“斯蒂格勒定律”，即“沒有一個科學(xué)發(fā)現(xiàn)是以最初發(fā)現(xiàn)者的名字來命名”。斯蒂格勒定律本身就符合這一定律，因為斯蒂格勒認(rèn)為這個定律是默頓（Robert Merton，1910—2003）首先提出的。楊-米爾斯理論也符合斯蒂格勒定律，——泡利在1953年就得到了一個類似的理論。日本物理學(xué)家內(nèi)山龍雄（1916—1990）為了統(tǒng)一萬有引力和電磁力，在1954年獨(dú)立提出了非交換規(guī)范場論。他曾在京都大學(xué)作報告，但沒有得到聽眾的積極回應(yīng)。得知楊-米爾斯的工作后，內(nèi)山龍雄在1955年把自己的論文修改成為一個更廣泛的規(guī)范場論，并在1956年發(fā)表。比楊振寧和米爾斯稍晚，薩拉姆（Abdus Salam，1926—1996）的學(xué)生蕭（Ronald Shaw，1929—2016）在1955年也獨(dú)立發(fā)現(xiàn)了楊-米爾斯理論。

　　盡管泡利、內(nèi)山、蕭都獨(dú)立于楊振寧和米爾斯得到了非交換規(guī)范場論，但楊振寧和米爾斯毫無疑問應(yīng)當(dāng)獲得最大的榮譽(yù)。泡利和蕭的工作都沒有發(fā)表，因為他們對其中的物理圖景不甚明了。內(nèi)山發(fā)表論文在楊-米爾斯之后，且受到楊-米爾斯的影響。只有楊振寧和米爾斯將這個尚存瑕疵的理論率先發(fā)表出來，讓后來者得以在此基礎(chǔ)上進(jìn)行研究。一個經(jīng)常被提到的故事是，當(dāng)楊振寧在普林斯頓作楊-米爾斯理論的報告時，臺下的泡利不停地問他非阿貝爾規(guī)范玻色子的質(zhì)量是什么。泡利曾經(jīng)深入研究過這一問題，知道質(zhì)量應(yīng)該是零，而這是不可能的。楊振寧回答說他不知道，但泡利一再追問。楊振寧認(rèn)為泡利的敵意過重，干脆停止演講坐到臺下，場面一時十分尷尬。最后，奧本海默（J。 Robert Oppenheimer，1904—1967）說，“我們應(yīng)該讓楊振寧繼續(xù)講。”楊振寧才回到講臺上，而泡利也沒有問更多的問題。[2] 楊-米爾斯理論中的質(zhì)量問題直到六十年代才通過希格斯機(jī)制得到解決。

　　1945年，泡利在普林斯頓高等研究院慶祝他的45歲生日（圖源：CERN）

　　楊振寧和米爾斯建立了楊-米爾斯理論的數(shù)學(xué)形式，其物理應(yīng)用則應(yīng)歸功于后來者。然而，與楊-米爾斯理論有關(guān)的數(shù)學(xué)成為現(xiàn)代數(shù)學(xué)里一個重要組成部分。1969年，楊振寧在紐約州立大學(xué)石溪分校講授一門廣義相對論課程。一天，他在黑板上寫下廣義相對論所需要用到的黎曼曲率張量公式，突然發(fā)現(xiàn)這個公式很像楊-米爾斯理論里的一個公式。他十分震驚，便去請教數(shù)學(xué)系主任西蒙斯（James Simons，1938— ）。西蒙斯告訴他這兩個公式都是纖維叢（fiber bundle）上的聯(lián)絡(luò)（connection）。楊振寧被這一美妙的聯(lián)系深深地震撼了。[3]

　　楊振寧與西蒙斯（圖源：The Stony Brook Dialogues in Mathematics and Physics）

　　1975年，楊振寧同吳大峻（1933— ）發(fā)表一篇論文，把纖維叢的數(shù)學(xué)語言翻譯為楊-米爾斯理論的物理語言，引發(fā)了數(shù)學(xué)界和物理學(xué)界對彼此工作的濃厚興趣。這就是著名的吳-楊字典（Wu-Yang dictionary）。事實上，關(guān)于纖維叢與楊-米爾斯理論的關(guān)系，在吳-楊字典之前就有一些人提到。例如赫爾曼（Robert Hermann， 1931—2020）在1970年的一本專著中對此有詳細(xì)闡述。但此類工作沒有產(chǎn)生吳-楊字典那樣的影響，這或許也可以算作斯蒂格勒定律的一個例子。

　　吳-楊字典（圖源：I。 M。 Singer， Some problems in the quantization of gauge theories and string theories）

　　七十年代后期，辛格（Isadore Singer，1924—2021）把吳-楊字典介紹給數(shù)學(xué)界，引發(fā)了數(shù)學(xué)家們學(xué)習(xí)楊-米爾斯理論的熱潮。一大批嶄新的數(shù)學(xué)工作得以誕生，為數(shù)學(xué)發(fā)展提供了新的動力。以下簡要介紹其中一部分。

　　楊-米爾斯理論中出現(xiàn)了一個偏微分方程

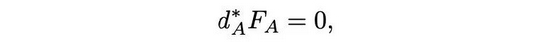
　　被稱為楊-米爾斯方程。1974年，楊振寧訪問其父楊武之（1896—1973）生前任教的復(fù)旦大學(xué)。他同谷超豪（1926—2012）、胡和生（1928— ）等人談起楊-米爾斯理論中的數(shù)學(xué)問題。雙方展開合作，在國際上率先對楊-米爾斯方程進(jìn)行研究，解決了該方程的許多基本問題。

　　1974年，谷超豪（左一）、胡和生（左二）與楊振寧開始合作研究規(guī)范場論（圖源：中國科學(xué)報）

　　1977-1978年，阿蒂亞（Michael Atiyah，1929—2019）、希欽（Nigel Hitchin，1946— ）和辛格證明了四維球面上楊-米爾斯方程的解的模空間是一個流形，并用指標(biāo)定理計算了其維數(shù)。1978年，阿蒂亞、希欽、德林菲爾德（Vladimir Drinfeld，1954— ）、馬寧（Yuri Manin，1937— ）四人合寫一篇論文，完全確定了這一模空間。

　　1982年，烏倫貝克（Karen Uhlenbeck，1942— ）證明了楊-米爾斯方程解的許多基本性質(zhì)，包括（四維的）可去奇點(diǎn)定理和（任意維數(shù)的）緊性定理。田剛（1958— ）和陶哲軒（1975— ）后來把可去奇點(diǎn)定理推廣到了高維。

　　烏倫貝克于1969年在伯克利（圖源：Oberwolfach Photo Collection）

　　1982年，陶布斯（Clifford Taubes，1954— ）發(fā)現(xiàn)了一種新的構(gòu)造楊-米爾斯方程解的方法，對于一大類四維流形證明了解的存在性。

　　復(fù)流形上楊-米爾斯方程的研究始于阿蒂亞和博特（Raoul Bott，1923—2005）在八十年代初的工作。小林昭七（1932—2012）和希欽猜測復(fù)流形上楊-米爾斯方程的解跟向量叢的穩(wěn)定性有關(guān)，這一猜想被唐納森（Simon Donaldson，1957— ）、烏倫貝克和丘成桐（1949— ）解決。受此啟發(fā)，丘成桐對復(fù)流形的凱勒-愛因斯坦度量作出類似猜想。田剛和唐納森進(jìn)一步闡述了丘成桐的猜想，引入了K-穩(wěn)定性的概念，在復(fù)幾何和代數(shù)幾何領(lǐng)域起到了核心作用。

　　1982年，丘成桐、阿蒂亞和希欽（圖源：Oberwolfach Photo Collection）

　　希欽在1987年定義了一維復(fù)流形上的希格斯叢，并研究了其上的楊-米爾斯方程。辛普森（Carlos Simpson，1962— ）把希欽的工作推廣到了高維。希格斯叢是近年來幾何拓?fù)漕I(lǐng)域的研究熱點(diǎn)，并且在數(shù)論和表示論中得到了出乎意料的應(yīng)用。吳寶珠（1972— ）使用希欽的工作證明了朗蘭茲綱領(lǐng)中的“基本引理”，并因此獲得2010年菲爾茲獎。1986年菲爾茲獎得主法爾廷斯（Gerd Faltings，1954— ）開創(chuàng)了p進(jìn)數(shù)域上希格斯叢的研究。卡普斯金（Anton Kapustin，1971— ）和威騰則使用希欽的工作（及其推廣）來研究幾何朗蘭茲綱領(lǐng)。

　　楊-米爾斯方程最著名的數(shù)學(xué)應(yīng)用是在低維拓?fù)漕I(lǐng)域。1983年，在烏倫貝克和陶貝斯工作的基礎(chǔ)上，唐納森使用楊-米爾斯方程研究四維流形的微分拓?fù)洌〉昧肆钊梭@異的結(jié)果。把唐納森和弗里德曼（Michael Freedman，1951— ）的工作結(jié)合起來，能夠證明四維空間R^4上有怪異的微分結(jié)構(gòu)，而這一點(diǎn)對其余維數(shù)的歐氏空間不成立。唐納森后來進(jìn)一步發(fā)展了他的理論，定義了光滑四維流形的不變量。唐納森因此獲得1986年菲爾茲獎。

　　2009年，唐納森（右二）和陶貝斯（右三）獲得邵逸夫數(shù)學(xué)獎（圖源：中國政府網(wǎng)）

　　1988年，弗洛爾（Andreas Floer，1956—1991）把唐納森理論發(fā)展到了三維流形上，定義了瞬子同調(diào)論。1998年，唐納森和他的學(xué)生托馬斯（Richard Thomas）使用SU（4）規(guī)范場論來研究卡拉比-丘三維復(fù)流形。2006年菲爾茲獎得主奧昆科夫（Andrei Okounkov，1969— ）和他的合作者們對唐納森-托馬斯理論有重要貢獻(xiàn)。

　　唐納森理論的思想如今在低維拓?fù)洹⑿翈缀巍⒋鷶?shù)幾何、復(fù)幾何等許多領(lǐng)域里都占據(jù)著主導(dǎo)地位，其后續(xù)發(fā)展包括格羅莫夫-威騰理論、塞伯格-威騰理論等等，盡管楊-米爾斯方程在這些理論里已經(jīng)不再出現(xiàn)。

　　楊-米爾斯方程在低維拓?fù)淅锏牧硗庖粋€應(yīng)用跟瓊斯多項式有關(guān)，這是瓊斯（Vaughan Jones，1952—2020）在1984年發(fā)現(xiàn)的一個新的紐結(jié)不變量。威騰在1989年指出，瓊斯多項式可以用楊-米爾斯理論來解釋。威騰的思想被雷希蒂欣（Nicolai Reshetikhin，1958— ）和圖拉耶夫（Vladimir Turaev，1952— ）發(fā)展為嚴(yán)格的數(shù)學(xué)理論，可以用來構(gòu)造一般三維流形的不變量。近二十年來，瓊斯多項式的一個推廣——霍瓦諾夫同調(diào)論（Khovanov homology）——成為低維拓?fù)淅锏难芯繜狳c(diǎn)。威騰同樣用楊-米爾斯理論給出了霍瓦諾夫同調(diào)論的一種解釋，引發(fā)了許多數(shù)學(xué)家的關(guān)注。

　　楊-巴克斯特方程

　　楊振寧另外一項對數(shù)學(xué)有深遠(yuǎn)影響的工作是楊-巴克斯特方程。這是一個形如

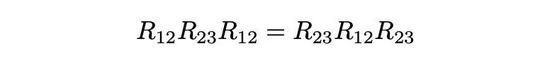
　　的矩陣方程，涉及了非線性可積物理模型的嚴(yán)格解。

　　楊-巴克斯特方程最早可以追溯到昂薩格（Lars Onsager，1903—1976）在1944年關(guān)于二維伊辛模型的工作，其中使用了星形-三角形方程。[4] 1963年，UCLA的一名博士生麥奎爾（James B。 McGuire，1934—2019）在研究一維量子多體問題時發(fā)現(xiàn)了類似的矩陣方程。楊振寧在1963年訪問UCLA時，跟麥奎爾討論了一維量子多體問題。當(dāng)時楊振寧已經(jīng)是名滿天下的諾貝爾獎得主，而麥奎爾僅僅是一個博士尚未畢業(yè)的無名小卒，然而楊振寧并未因此輕視麥奎爾的工作。受到麥奎爾的啟發(fā)，楊振寧在1967年和1968年的兩篇論文里提出了現(xiàn)今形式的楊-巴克斯特方程。后來巴克斯特（Rodney Baxter，1940— ）在1971年和1972年的兩篇統(tǒng)計力學(xué)論文里也獨(dú)立發(fā)現(xiàn)了此方程。

　　楊振寧與巴克斯特在楊振寧退休慶祝會議上（圖源：Symmetry and Modern Physics - Yang Retirement Symposium， 1999）

　　七十年代末，法捷耶夫（Ludvig Faddeev，1934—2017）領(lǐng)導(dǎo)的蘇聯(lián)數(shù)學(xué)物理學(xué)派將這一方程命名為楊-巴克斯特方程，并深入研究其在數(shù)學(xué)和物理里的應(yīng)用。受他們工作的影響，德林菲爾德和神保道夫（1951— ）開始了“量子群”的研究。德林菲爾德甚至將一類量子群命名為“楊代數(shù)”（Yangian），以紀(jì)念楊振寧的貢獻(xiàn)。

　　楊-巴克斯特方程可以看作是數(shù)學(xué)中“辮群”的一個基本關(guān)系，能夠用如下“辮子”的圖像來表示。

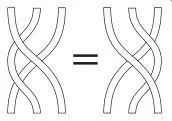
　　上圖中的辮子關(guān)系在紐結(jié)的瓊斯多項式里起到重要作用。圖拉耶夫發(fā)現(xiàn)，包括瓊斯多項式在內(nèi)的許多紐結(jié)不變量都可以從楊-巴克斯特方程的解得到。雷希蒂欣和圖拉耶夫進(jìn)一步的工作則是使用量子群來構(gòu)造紐結(jié)不變量。

　　西蒙斯幾何與物理中心的墻上鐫刻著一些基本的物理公式，圖中左下角即楊-巴克斯特方程（圖源：西蒙斯幾何與物理中心）

　　1990年四位菲爾茲獎得主中，德林菲爾德、瓊斯和威騰的（部分）獲獎工作都跟楊-米爾斯理論和楊-巴克斯特方程有密切關(guān)系。森重文（1951— ）是一位代數(shù)幾何學(xué)家，他的獲獎工作跟物理沒有直接聯(lián)系。近年來許晨陽（1981— ）等人的工作把森重文開創(chuàng)的極小模型綱領(lǐng)同K-穩(wěn)定性結(jié)合起來，而K-穩(wěn)定性很大程度上是受楊-米爾斯理論啟發(fā)而建立起來的。

　　1990年四位菲爾茲獎得主，左起：威騰、森重文、瓊斯、德林菲爾德（圖源：ICM2002.org.cn）

　　李-楊單位圓定理

　　李政道與楊振寧在1952年發(fā)表了兩篇統(tǒng)計力學(xué)方面的論文，其中證明了某一類配分函數(shù)的零點(diǎn)都在單位圓上，這就是著名的李-楊單位圓定理。愛因斯坦對這一工作非常感興趣，邀請李楊二人到他的辦公室去討論了一個半小時。[5]李-楊定理依賴于一個純數(shù)學(xué)結(jié)果，即某一類多項式所有零點(diǎn)都在單位圓上。為了證明這一結(jié)果，李楊二人翻閱了哈代（G。 H。 Hardy，1877—1947）、李特爾伍德（John Littlewood，1885—1977）、波利亞（George Pólya，1887—1985）所著的《不等式》一書，還咨詢了馮·諾伊曼（John von Neumann，1903—1957）和塞爾伯格（Atle Selberg，1917—2007）等同事。卡茨（Mark Kac，1914—1984）當(dāng)時在普林斯頓高等研究院訪問，他聽到李楊的問題后，立刻想到了波利亞一篇關(guān)于黎曼假設(shè)的論文，并用其中的方法證明了李楊所需結(jié)果最簡單的情形。卡茨將此事告知了李楊。受此啟發(fā)，楊振寧和李政道繼續(xù)研究了幾個星期，終于用卡茨的方法以及數(shù)學(xué)歸納法證明了最廣泛的情形。[6]

　　1957年，李政道和楊振寧在普林斯頓高等研究院（圖源：IAS Archives）

　　李-楊單位圓定理是統(tǒng)計力學(xué)里的重要工作，但它對數(shù)學(xué)的影響遠(yuǎn)不能同楊-米爾斯理論和楊-巴克斯特方程相提并論。然而，這個定理的敘述跟黎曼假設(shè)非常相像。如果作一個變量替換，就能把李-楊定理敘述成：某一類配分函數(shù)的零點(diǎn)都在虛軸上。黎曼假設(shè)說的是黎曼ζ函數(shù)

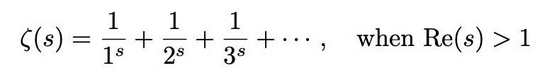
　　的非平凡零點(diǎn)都在直線Re（s）=1/2上。故此，有一部分?jǐn)?shù)學(xué)家希望能夠把黎曼ζ函數(shù)表示為某個物理系統(tǒng)的配分函數(shù)，從而研究黎曼假設(shè)。（用物理方法研究黎曼假設(shè)是當(dāng)前的一個流派，這方面更常見的工作是將量子力學(xué)與黎曼ζ函數(shù)聯(lián)系起來。）

　　楊振寧的純數(shù)學(xué)工作

　　楊振寧曾多次表示，如果自己不做物理，一定會去做數(shù)學(xué)。[5，7] 事實上，除了數(shù)學(xué)物理方面的眾多成果以外，楊振寧也發(fā)表過一些純數(shù)學(xué)論文。這些工作對于楊振寧這樣的科學(xué)巨人來說無足輕重。然而，從這些論文中可以看出，跟許多其他理論物理學(xué)家不同，楊振寧也可以有跟數(shù)學(xué)家一樣的品味，使用跟數(shù)學(xué)家一樣的語言。楊振寧發(fā)表的第一篇論文就是純數(shù)學(xué)論文。這是他在西南聯(lián)大時寫的，題為“On the uniqueness of Young‘s differentials”（Young微分的唯一性），1944年發(fā)表在《美國數(shù)學(xué)會通報》（Bulletin of the American Mathmatical Society）上。這篇論文的水平不高，楊振寧對它也很不滿意。楊振寧最初僅僅是把它當(dāng)作學(xué)習(xí)微積分的課外練習(xí)，幾年后才在授課老師曾遠(yuǎn)榮（1903—1994）的建議下投寄出去發(fā)表。[8]楊振寧的父親楊武之教授在芝加哥大學(xué)獲得博士學(xué)位，歸國后任教于清華大學(xué)數(shù)學(xué)系，是中國數(shù)論研究的先驅(qū)。在楊武之的博士論文里，他考慮了華林問題的一個變種：求最小的k，使得任何一個自然數(shù)能夠表示為最多k個“金字塔數(shù)”之和。這里的“金字塔數(shù)”指形如

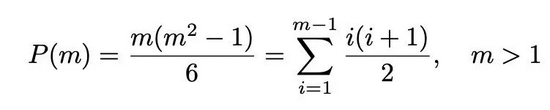
　　的數(shù)。楊武之證明了k不超過9，這一結(jié)果后來被人改進(jìn)為8。

　　1993年，楊振寧和鄧越凡（1962— ）用計算機(jī)研究了這一問題，發(fā)現(xiàn)十億以內(nèi)的自然數(shù)都能表示為至多5個金字塔數(shù)之和，并且其中足夠大的數(shù)表示為至多4個金字塔數(shù)之和。據(jù)此，他們猜想足夠大的自然數(shù)都能表示為至多4個金字塔數(shù)之和。他們進(jìn)一步猜想了能表示為至多k個金字塔數(shù)之和的自然數(shù)的個數(shù)的漸進(jìn)公式。

　　楊振寧與陳省身

　　陳省身（1911—2004）和楊振寧兩位先生是二十世紀(jì)華人科學(xué)家中的翹楚。他們兩人私交甚篤，在學(xué)術(shù)上也有密切聯(lián)系。陳省身1930-1934年間在清華大學(xué)擔(dān)任助教和攻讀研究生，同楊武之教授有師生之誼。陳省身與夫人鄭士寧的婚事就是楊武之夫婦介紹的。陳省身曾多次到楊武之家中吃飯，見到過年僅八歲的楊振寧，但楊振寧對陳省身并無印象。[3，9] 后來楊振寧在西南聯(lián)大求學(xué)期間，曾經(jīng)選修過陳省身開設(shè)的多門課程，包括微分幾何。[3]

　　陳省身是纖維叢和聯(lián)絡(luò)理論的主要推動者。他的陳-韋伊理論把楊-米爾斯方程中的曲率項同陳示性類聯(lián)系起來，而陳-西蒙斯理論也跟楊-米爾斯理論密不可分。1975年，理解了楊-米爾斯理論與纖維叢的關(guān)系后，楊振寧驅(qū)車到陳省身家中，同他談起此事，說：“這既令我驚訝，也令我迷惑不解，因為你們數(shù)學(xué)家憑空夢想出這些概念。”陳省身當(dāng)即提出異議：“非也，非也，這些概念并非是憑空夢想出來的，它們既是自然的，也是實在的。”[3]

　　陳省身先生1985年在南開大學(xué)創(chuàng)建了南開數(shù)學(xué)研究所，他邀請楊振寧于1986年在所內(nèi)建立了理論物理研究室。經(jīng)楊振寧推薦，葛墨林（1938— ）具體負(fù)責(zé)理論物理研究室的工作。這一研究室主要的研究方向便是與楊-米爾斯理論和楊-巴克斯特方程相關(guān)的數(shù)學(xué)。

　　楊振寧在七十年代寫下一首詩《贊陳氏級》，在數(shù)學(xué)與物理學(xué)界廣為流傳：

　　天衣豈無縫，匠心剪接成。渾然歸一體，廣邃妙絕倫。造化愛幾何，四力纖維能。

　　千古寸心事，歐高黎嘉陳。

　　其中最后一句稱贊陳省身是可以與歐幾里得（Euclid，公元前3世紀(jì)）、高斯（Carl Friedrich Gauss，1777—1855）、黎曼（Bernhard Riemann，1826—1866）、嘉當(dāng)（élie Cartan，1869—1951）并肩的幾何學(xué)家。

　　2002年，江才健出版了《楊振寧傳-規(guī)范與對稱之美》。陳省身先生也賦詩一首作為序言：

　　以詩代序

　　愛翁初啟幾何門，

　　楊子始開大道深。

　　物理幾何是一家，

　　炎黃子孫躋西賢。

　　注：愛因斯坦的廣義相對論將物理釋為幾何。規(guī)范場論作成大道，令人鼓舞。

　　兩位大師盡管身處不同領(lǐng)域，但他們的偉大工作相得益彰，堪稱佳話。

　　楊振寧（攝影：鄧偉）

　　[參考文獻(xiàn)]

　　[1] 張?zhí)烊兀?/p>

　　外爾與楊振寧——物理的真與數(shù)學(xué)的美 | 量子群英會

　　[2] Mikhail Shifman，非阿貝爾規(guī)范場的起源與爭執(zhí)：關(guān)于泡利與楊振寧的軼事

　　[3] 張奠宙，楊振寧如何看待數(shù)學(xué)與物理

　　[4] Helen Au-Yang and Jacques H。 H。 Perk， Onsager‘s Star-Triangle Equation： Master Key to Integrability， Advanced Studies in Pure Mathematics 19， 1989 Integrable Systems in Quantum Field Theory and Statistical Mechanics

　　[5] 劉鈍、王浩強(qiáng)訪問整理，愛因斯坦、物理學(xué)和人生——楊振寧先生訪談錄

　　[6] Mark Kac， Comments on G。 Pólya‘s “Bemerkung uber die integraldarstellung der Riemannschen zeta-funktion”

　　[7] 華東師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，楊振寧專程看望數(shù)學(xué)科學(xué)學(xué)院張奠宙先生

　　[8] 施郁，楊振寧對西南聯(lián)大的新回憶

　　[9] 陳省身，我與楊家兩代的因緣