|
不支持Flash
|
|
|
|
DCE與CBOT黃豆期價關聯性及動態走勢實證研究http://www.sina.com.cn 2006年10月13日 00:45 大連商品交易所
摘要:本文采用協整理論以及基于VAR的Grange 因果關系檢驗方法對中國大連商品交易所黃豆期貨價格作建模分析。單位根檢驗顯示,選取的周樣本序列均為I(1)。Granger因果關系檢驗顯示:CBOT黃豆期貨價格為大連黃豆期價的單向的Granger原因;大連黃豆期貨價格是黑龍江、大連黃豆現貨價格單向的Granger原因;美元匯率變量與大連黃豆期價之間不存在Granger因果。長期協整方程顯示:CBOT黃豆期貨價格、大連黃豆現貨價格、美元指數與大連黃豆期價構成長期顯著的均衡關系;美黃豆連續期價對大連黃豆期價的彈性是0.13,大連黃豆現貨價格對大連黃豆期價的彈性是0.13,美元指數對大連黃豆期價的彈性分別為-0.48。從最終建立動態模型來看,模型有較好的擬合及預測精度。因此,該模型對國內黃豆期價風險控制具有較好的參考作用。 關鍵詞:黃豆期價; 美元匯率; 協整; 動態預測; Empirical Study About Correlation And Dynastical Trend Of Soybean Futures Prices Between Dalian and CBOT Abstract: In this paper, we made model-building analyze to prices of Soybean futures of Da Lian Commodity Exchange through Cointegration theory and Grange Causality testing which based on VAR. Unit-Root-Testing results show that Time series data, which were selected, are I(1). Grange causality testing show that Soybean Futures price of CBOT is single directional Granger cause of Soybean futures prices of Dalian, and Soybean futures prices of Dalian is single directional Granger cause of Heilongjiang’s and Dalian’s Soybean spot prices. Cointegration testing showed that Soybean Futures price of CBOT and Soybean Spot prices and Exchange rate of Euro have long-term marked equilibrium relationship with Soybean futures prices of Dalian. The elasticity of Soybean Futures price of CBOT to Soybean futures prices of Dalian is 0.13. The elasticity of Soybean Spot prices of Heilongjiang to Soybean futures prices of Dalian is 0.13 and dollar index to Soybean futures prices of Dalian is -0.48. ECM models have good statistical property and good fitness and forecasting premise. Therefore, the models have good consultation function to forecast and control futures prices of Dalian Soybean risk. Key Words: Soybean Futures Prices, Exchange Rate of Dollar, Cointegration, Dynamic Forecasting. 從定性的角度,我們可以看到大連商品交易所的黃豆期貨同CBOT黃豆期貨之間存在較強的關聯性,一般的對國內的黃豆期貨走勢的技術分析和基本面分析,通常都要參考于外盤,主要是CBOT黃豆期貨市場的變化。我們知道影響國內黃豆期貨價格走勢的因素有很多,諸如,供給與需求因素,天氣因素,外盤的變化等等。為了進一步對國內黃豆期貨價格走勢作定量分析,我們撇開其它因素,僅從外盤的變化考慮,作定量模型研究。 目前,國際黃豆價格的波動給國內黃豆市場帶來較大的沖擊影響,從而給國內生產及消費企業帶來一定的風險。如何規避黃豆價格波動風險,確保生產的有序運行顯得極為迫切。本文采用協整理論及基于VAR的Grange 因果關系檢驗方法及沖擊反應函數及方差分解的方法研究國內外黃豆期貨價格關聯性及對未來走勢作出預測研究,以期對生產及消費提供理論及實踐的指導作用。 一、文獻綜述及研究進展 國內外對期貨市場交易及其規律的研究由來已久。尤其是近年來,從經濟建模的角度研究期貨市場的規律是一個發展方向。 從國內來看,由于期貨市場規范發展時間不長,對期貨市場的運行規律及風險控制的研究多是集中在定性的角度,從定量的角度研究的還不多,尤其對金屬期貨市場的研究文獻較少。已有的文獻諸如:吳沖鋒等(1994)在國外三種基本期貨價格模型的基礎上,提出了上海期貨交易所期貨價格的改進模型。華仁海和仲偉俊(2002)使用協整的方法,運用上海期貨交易所的銅和鋁價格數據以及華通有色金屬市場、長江有色金屬市場的現貨價格進行了分析。高輝(2004)以上海期貨交易所與英國倫敦金屬交易所(LME)為例,從實證的角度分析了中國期貨市場與國際期貨市場的關聯度,對上海期貨交易所銅期貨收盤價與未平倉手數之間的協整關系作了分析.發現上海期交易所銅期貨價格與現貨價格之間存在協整關系、期貨價格與現貨價格之間的收斂關系,證實了上海期貨市場的有效性.高輝(2004、2005)采用協整理論以及基于VAR的Grange 因果關系檢驗方法分別對中國上海期貨交易所期銅價格、天然橡膠生產及消費、現貨價格及期貨價格以及上海期貨交易所的燃料油期貨價格的形成機制等作建模分析,同時給出價格的動態預測,檢驗結果表明預測效果均較好。高輝(2005)采用協整模型、Granger因果關系檢驗、ECM模型及幾種GARCH模型對中國上海與英國倫敦的期貨價格及收益率和波動性做了實證分析。發現兩市期貨價格之間存在雙向的Granger因果關系和顯著的協整關系。兩個市場之間存在顯著的同向變動關系和長期的共同趨勢。兩市的長期期貨價格收益率幾乎沒有顯著差異,兩市均受到對方市場期貨價格收益率的影響,短期波動過程存在著一定的差異。建立的GARCH類模型發現,兩市在波動性的傳導和影響上存在一定程度的非對稱性且兩市均存在溢出效應與一定的杠桿效應。上海期貨市場對倫敦期貨市場的溢出效應顯著存在,而倫敦期貨市場對上海期貨市場的溢出效應不顯著存在。市場的波動性對消息影響呈現一定程度的非對稱性。兩市存在的利空消息均大于利多消息的作用。 從國外來看,對期貨價格的定量研究較多。尤其是近年來,協整等時間序列理論的發展極大地推動了關于期貨研究的進程。 Engle&Granger(1987)發展的嶄新EG兩步法,以及Johansen(1988)提出了向量自回歸模型為基礎的協整檢驗方法, Shen &Wang (1990)首次運用Engle 和Granger(1987)提出的協整的方法來檢驗期貨市場的價格發現。此后,LaiKS& LaiMA(1991),Schroeder (1991) & Quan J (1992) 分別對遠期外匯、生豬、原油期貨市場的價格發現功能作出了一系列實證分析。Fatimah MohdArshad & Zainalabidin Mohamed(1993)運用協整的方法實證分析了棕櫚油期貨市場的定價效率問題。 Jian Yang &David ABessler & David JLeatham(2001)把協整方法運用到研究商品的可儲存性和商品期貨市場的價格發現中,他們認為商品的可儲存性可能對于期貨價格對于現貨價格預測的精確度是有影響的。隨后GARCH類模型的發展,廣泛運用于期貨市場。諸如:Jian Yang , Michael S. Halgh & David J. Leatham(2001)通過GARCH模型模擬農產品期貨價格的波動性。Michael D. Mckenzie , Heather Mitchell(2001),采用ARCH系列模型ARCH模型、GARCH模型和AP-GARCH模型來對LME所有期貨合約的價格波動性,進行模擬。D. E. Allen,S. N. Cruickshank(2002)使用ARCH對悉尼商品交易所,倫敦國際金融期貨和期權交易所以及新加坡國際金融交易所的商品期貨的波動性進行建模。 綜上,從國內外已有的文獻看,對期貨規律的定量研究基本是建立在簡單線性回歸模型以及時間序列建模角度。尤其是協整理論的發展,為研究期貨市場規律提供了新的思路。因此,本文試圖利用協整理論,基于向量自回歸(VAR)的Granger 因果關系檢驗以及沖擊響應函數方法,從多變量的角度對國內外黃豆的期貨價格關系及未來走勢做建模研究,期望獲得有益的結論。 二、協整及相關理論 (一)“協整”的概念 在經濟領域內,作建模研究,以往的建模技術均存在著動態的穩定性假設,即以時間序列為依據的經驗分析,都假定時間序列是平穩的(Stationary)。廣義地說,如果一個隨機過程的均值和方差在時間過程上都是常數,并且在任何兩個時期之間的協方差僅依賴于該兩個時期之間的距離或滯后,而不依賴于計算這個協方差的實際時間,就稱其為平穩。實際上,經濟時間序列通常都是非平穩的,基于一個穩定的模型而使用非穩定的時間序列數據來建模,體現了以往建模技術一定的在經濟領域應用的局限性,而“協整”技術正好彌補了這一穩定假設的不足。“協整”(Cointegration),最初由Granger在1981年提出概念性設想,后由Engle與Granger一起在1987年提出嚴謹的定理證明及具體的可操作框架。 “協整”是描述時間序列之間長期關系的一種統計性質。考慮兩個或多個I(1)序列 ,一般它們的線性組合仍然是I(1)的,但如果存在某個線性組合,使新得到的序列是平穩的,那么就說這幾個時間序列之間是“協整”的(cointegrated)。組合中序列的系數為協整向量。用規范化的語言表述即:對于時間序列 (1) (2)存在一個非零常量 ,使得 變量協整性分析的經濟意義在于:對于兩個具有各自長期波動規律的變量,如果它們之間是協整的,則它們之間存在一個長期的均衡關系。反之,如果這兩個變量不是協整的,則它們之間不存在一個長期的均衡關系。 (二)單位根檢驗與因果關系檢驗 1、單位根檢驗 Dickey, Fuller(1981)在DF檢驗 的基礎上進行了擴展,通過假定其序列是一個P階自回歸過程,增加一個滯后的差分項來解決誤差項
如果一個原始序列平穩,我們稱之為I(0)過程。如果一個原始時間序列不平穩,而經過一階差分變成平穩的,我們就說原始(隨機)序列是一階單整,簡稱I(1)。 Dickey, Fuller(1979)提出考慮一階自回歸基礎上DF檢驗,檢驗方程 在ADF檢驗中存在一個問題,即檢驗回歸中包括常數,常數和線性趨勢,或二者都不包括。選擇標準為:如序列好像包含有趨勢(確定的或隨機的),在序列回歸中應既有常數又有趨勢;如序列沒表現任何趨勢且有非零均值,在回歸中應僅有常數;如序列在零均值波動,在檢驗回歸中應既不含有常數又不含有趨勢。 另外,Phillips和Perron(1988)提出一種非參數方法來控制序列中高階序列相關,即PP法。它不再嚴格要求 PP統計量: q是截斷滯后因子,檢驗假設: 2、因果關系(Causal Relationship)檢驗 因果關系檢驗是由Granger提出的,其基本思想是:設 分別表示它們到時刻t的整個時間序列。若用 這里 (三)“協整”關系的檢驗與估計 關于協整關系的檢驗與估計,目前有許多具體的技術模型,如EG兩步法,Johansen極大似然法,Gregory Hansan(1996)法,自回歸分布滯后模型( ARDL)方法,頻域非參數譜回歸法,Bayes方法等等。 Engle和Granger建議使用兩階段回歸法解決時間序列的非平穩性,由于此方法易于計算,因而早期被廣泛采用,但其缺點是在小樣本下,參數估計的誤差較大,并且當變量超過兩個以上時,變量間可能存在多個“協整”關系,此方法無法找到所有可能的協整向量,其分析結果不易解釋。Johansen(1988)針對上述問題提出極大似然估計法(MLE),Gonzalo利用模擬分析所獲得的結果顯示,Johansen檢驗優于Engle和Granger的方法。本文即采用Johansen檢驗法。 Johansen方法檢驗變量間是否具有協整關系的特點:是對三個或者三個以上的變量間協整關系個數不作先驗的假定,協整關系個數只是假設檢驗的結果。 Johansen(1988), Johansen,Juselius(1990)認為可以用特征根最大值統計量與跡統計量來判斷是否存在協整關系,給定“最多具有r個協整關系”的原假設。如果該統計量超過臨界值,則拒絕原假設,即有r+1個協整關系。 協整檢驗的目的是,決定一組非穩定序列是否是協整的。如下面所解釋的,協整關系的出現形成VEC說明的基礎,給以VAR為基礎的協整檢驗提供的工具是Johansen (1991, 1995a) 發展的方法論,VAR模型是由Sims (1972,1980)首先發展的,VAR模型的核心思想就是不考慮經濟理論,而直接考慮作為時間序列的各經濟變量間的關系。考慮階數為p的VAR模型: 其中, 其中 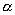 中的元素是向量誤差修正模型VEC中的調整參數。Johansen方法是在無約束VAR的形式下估計 中的元素是向量誤差修正模型VEC中的調整參數。Johansen方法是在無約束VAR的形式下估計 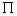 矩陣,然后求出 矩陣,然后求出 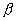 ,從而檢驗出協整秩,(秩 ,從而檢驗出協整秩,(秩 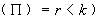 ),得出協整向量。 ),得出協整向量。
Johansen的跡統計量為: (四)誤差校正模型與沖擊反應分析 根據Granger表達定理,協整系統有三種等價的表達形式:向量自回歸VAR、移動平均MA和誤差修正模型(Error Correction Model, ECM),其中ECM最能直接描述短期波動與長期均衡的綜合,應用最為普遍。 向量誤差修正模型(VEC)是一個有約束的VAR模型,并在解釋變量中含有協整約束,因此它適用于已知有協整關系的非平穩序列。當有一個大范圍的短期動態波動時,VEC表達式會限制內生變量的長期行為收斂于它們的協整關系。因為一系列的部分短期調整可以修正長期均衡的偏離,所以協整項被稱為是誤差修正項。 誤差校正模型是短期動態模型。為方便起見,考慮一個只有兩個變量的ADL(p,q)模型: 經過簡單的變換得到誤差校正表示形式: 誤差校正模型(5.9)只是方程(5.8)的適當變形,它與方程(5.8)是等價的,采用誤差校正的形式有許多優點 ,因此,變量序列不平穩的時候,采用ECM可以避免偽回歸的問題,序列協整時,應該建立誤差校正模型,這時只能采用差分后的變量建模。經濟中許多變量序列是不平穩的,而且經濟理論往往假設某些變量之間存在長期均衡關系,因此可以采用協整和誤差校正方法建立模型。 根據Ender(1995)的研究,一個時間序列預測的誤差方差是自身擾動及系統其他擾動共同作用的結果。沖擊分解的目的就是研究一個系統中,當某一擾動發生時,系統隨后的變動多大程度是受到該擾動的影響。沖擊響應函數刻畫的是在擾動項上加一個標準差大小的沖擊,對于內生變量當前值和未來值所帶來的影響。對一個變量的沖擊直接影響這個變量,并且通過VEC模型的動態結構傳導給其它所有的內生變量。 為了對我國宏觀經濟變量的動態特性有一個清楚的了解,應用上面的VEC模型,對經濟變量進行沖擊響應(impulse response)分析,即計算1個單位的各種沖擊對中國天然橡膠生產、消費及交易的宏觀經濟變量的影響,相應地作出沖擊響應曲線。 (五)模型穩定性檢驗 在建模過程中,時間序列中往往存在著一些斷點,由于斷點的存在對模型的穩定性影響很大,因而最后對模型的穩定性進行檢驗十分必要。Brown,Durbin,Evans(1975)提出累積平方和檢驗(CUSUMSQ),檢驗統計量為: CUSUMSQ(s)= 其中: 鄒檢驗是常用的結構變化檢驗,檢驗統計量為: 其中: Quandt(1960)、 Hansen(1992)、Andrews,Ploberger(1994)分別提出了基于鄒檢驗的擴展檢驗,在斷點未知的情況下確定斷點發生的時間,并給出了檢驗統計量與分布,結論為:未知斷點的檢驗統計量為: 其中: 綜上所述,我們對協整建模相關理論進行了適當的總結和回顧,目的是為有關研究做理論鋪墊。以下我們將具體運用協整及相關理論,對影響中國大連黃豆期價的若干因素,做定量的模型研究。
【發表評論】
|
不支持Flash
不支持Flash
|
||||||||||||||||
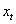 ,
, 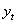 ,如果它們滿足下述條件,則它們是協整的:
,如果它們滿足下述條件,則它們是協整的:
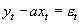 ~I(0), 即是平穩的。
~I(0), 即是平穩的。
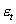 的高階序列相關問題,稱之為ADF單位根檢驗(Unit Root Testing)。即檢驗方程:
的高階序列相關問題,稱之為ADF單位根檢驗(Unit Root Testing)。即檢驗方程:
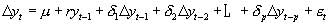 ( 1)
( 1)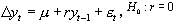 。
。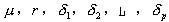 為參數, 為隨機誤差項,是服從獨立同分布(iid)的白噪聲過程,假設
為參數, 為隨機誤差項,是服從獨立同分布(iid)的白噪聲過程,假設 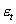 。若
。若 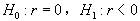 ,則變量服從單位根過程,是非平穩的。若
,則變量服從單位根過程,是非平穩的。若 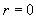 被拒絕,則是平穩的。在ADF檢驗中,我們采用滯后長度的選取標準是:在保證殘差項不相關的前提下,同時采用AIC 準則與Schwarz信息標準,即SC準則,作為最佳時滯的標準。在二者值同時為最小時的滯后長度即為最佳長度。
被拒絕,則是平穩的。在ADF檢驗中,我們采用滯后長度的選取標準是:在保證殘差項不相關的前提下,同時采用AIC 準則與Schwarz信息標準,即SC準則,作為最佳時滯的標準。在二者值同時為最小時的滯后長度即為最佳長度。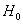 是獨立同分布。PP法是通過一階自回歸項系數的t統計量進行修正來解決誤差項
是獨立同分布。PP法是通過一階自回歸項系數的t統計量進行修正來解決誤差項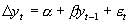 ( 2)
( 2)
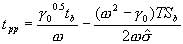 ,
, 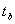 是
是 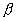 的t統計量,
的t統計量, 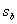 是
是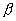 標準差,
標準差, 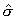 是檢驗回歸標準差,T是檢驗的時間長度,
是檢驗回歸標準差,T是檢驗的時間長度,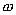 是Newey-West異方差,自回歸一致估計由下式給出:
是Newey-West異方差,自回歸一致估計由下式給出: 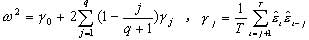 ( 3)
( 3)
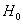 :變量服從單位根過程,是非平穩的。
:變量服從單位根過程,是非平穩的。 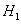 :變量不服從單位根過程,是平穩的。當
:變量不服從單位根過程,是平穩的。當 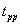 值小于臨界值時,就接受
值小于臨界值時,就接受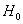 ,反之,就拒絕
,反之,就拒絕 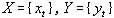 為兩個隨機時間序列,并令:
為兩個隨機時間序列,并令:
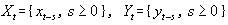
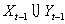 預測
預測 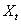 ,比用
,比用 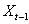 預測更準確,則認為
預測更準確,則認為 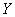 對
對 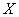 具有因果關系。反之亦然。Geweke,Meese和Dent提出了檢驗因果關系的數學模型:
具有因果關系。反之亦然。Geweke,Meese和Dent提出了檢驗因果關系的數學模型: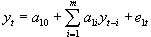 (4)
(4)
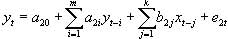 (5)
(5)
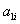 和
和 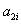 是
是 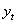 與
與 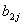 是
是 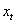 值及其滯后值的回歸系數,
值及其滯后值的回歸系數, 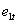 和
和 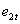 是白噪聲。檢驗從
是白噪聲。檢驗從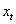 到
到 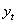 單向因果關系,即是檢驗對
單向因果關系,即是檢驗對 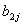 的零假設
的零假設 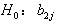 =0(j=1,2,…,k)。診斷統計量為:
=0(j=1,2,…,k)。診斷統計量為: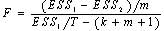 ,式中
,式中 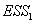 和
和 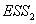 分別上述模型最小二乘法回歸方程中的殘差的平方和,T是時間序列
分別上述模型最小二乘法回歸方程中的殘差的平方和,T是時間序列 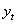 的樣本數。在置信概率α下,若
的樣本數。在置信概率α下,若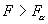 ,則拒絕
,則拒絕 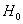 假設,認為
假設,認為 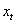 對
對 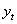 有因果關系。
有因果關系。
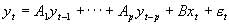 (6)
(6)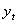 是一個含有非平穩的I(1)變量的
是一個含有非平穩的I(1)變量的 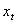 維向量;
維向量; 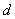 是一個確定的 維的向量,
是一個確定的 維的向量, 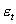 是擾動向量。我們可把VAR重寫為以下形式:
是擾動向量。我們可把VAR重寫為以下形式:
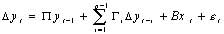 (7)
(7)
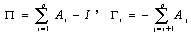 。Granger定理指出:如果系數矩陣∏的秩
。Granger定理指出:如果系數矩陣∏的秩 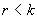 ,那么存在
,那么存在 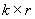 階矩陣
階矩陣 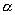 和
和 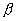 ,它們的秩都是
,它們的秩都是 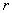 ,使得
,使得 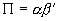 ,并且
,并且 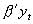 是穩定的。其中
是穩定的。其中 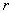 是協整關系的數量(協整秩)并且
是協整關系的數量(協整秩)并且 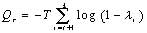 ,其中:k 是所檢驗的一組序列包含的序列個數,
,其中:k 是所檢驗的一組序列包含的序列個數, 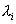 是第i步最大特征根,而r是假設的協整關系個數,
是第i步最大特征根,而r是假設的協整關系個數, 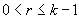 。檢驗假設:
。檢驗假設: 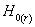 :在這一組序列中至多存在r個協整關系。
:在這一組序列中至多存在r個協整關系。 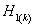 :至多有k個協整關系。由于在k序列組成的協整檢驗中,不可能存在k個協整關系,即協整向量矩陣不可能是滿秩的 ,因此,備擇假設表明,不存在協整關系。
:至多有k個協整關系。由于在k序列組成的協整檢驗中,不可能存在k個協整關系,即協整向量矩陣不可能是滿秩的 ,因此,備擇假設表明,不存在協整關系。
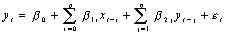 (8)
(8)
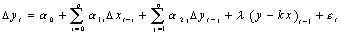 (9)
(9)
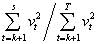 (10)
(10)
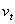 為回歸殘差,T是樣本總量,k是估計參數的數量。基于遞歸最小二乘法對穩定性檢驗,除了CUSUMSQ檢驗外,還有CUSUM檢驗、一步預測檢驗、N步預測檢驗、遞歸系數估計檢驗。
為回歸殘差,T是樣本總量,k是估計參數的數量。基于遞歸最小二乘法對穩定性檢驗,除了CUSUMSQ檢驗外,還有CUSUM檢驗、一步預測檢驗、N步預測檢驗、遞歸系數估計檢驗。
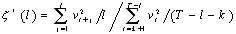 (11)
(11)
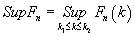 (12)
(12)
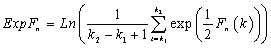 (13)
(13)
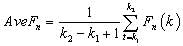 (14)
(14)
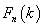 為鄒檢驗統計量,
為鄒檢驗統計量, 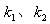 為所要檢驗的斷點發生的時間范圍。Hansen(1997)提供了相關的GAUSS程序,并給出了樣本統計量p值。
為所要檢驗的斷點發生的時間范圍。Hansen(1997)提供了相關的GAUSS程序,并給出了樣本統計量p值。