來源：量子位

夢晨 蕭簫 發(fā)自 凹非寺

量子位 報(bào)道 | 公眾號(hào) QbitAI

劉慈欣的科幻小說《三體》，讓很多人知道了“三體問題”這一世紀(jì)難題。

這個(gè)問題，最初由牛頓提出。

當(dāng)時(shí)，在用萬有引力定律解釋了行星(如地球)如何繞太陽運(yùn)動(dòng)的“二體問題”后，牛頓又想到了一個(gè)進(jìn)階問題：

在太陽和地球的雙重影響下，月球如何繞地球運(yùn)動(dòng)？

于是，他在《自然哲學(xué)的數(shù)學(xué)原理》中提出了三體問題：

三個(gè)可以視為質(zhì)點(diǎn)的天體，在其相互之間的萬有引力作用下，應(yīng)該如何運(yùn)動(dòng)？

牛頓的經(jīng)典力學(xué)，描述了一個(gè)決定論的世界。拉普拉斯曾斷言：“只要知道宇宙中所有粒子的當(dāng)前位置和速度，原則上就有可能預(yù)測任何時(shí)刻的情況。”

本以為只是二體問題之上再加一個(gè)體而已，很快就能解決。

沒想到，牛頓根本找不到這個(gè)問題的通用解！

幾代科學(xué)家經(jīng)過努力，也只找出三體問題在一些限制條件下的特殊解。

例如位于非等邊三角形頂點(diǎn)的三個(gè)等質(zhì)量質(zhì)點(diǎn)，在初速度為0時(shí)的運(yùn)動(dòng)規(guī)律，幾乎毫無章法。

牛頓之后，歐拉、拉格朗日、泊松等許多數(shù)學(xué)家都向三體問題發(fā)出挑戰(zhàn)，但依然找不出它的通用解。

三體問題難在哪里？

其實(shí)，早期的科學(xué)家根本沒有意識(shí)到，他們試圖解決的三體問題難度有多么恐怖。

直到1885年，瑞典數(shù)學(xué)雜志Acta Mathematica舉辦了一次國際數(shù)學(xué)大賽，其中第一道題是比三體問題還難的N體問題。

對于一個(gè)根據(jù)牛頓定律相互吸引的多質(zhì)點(diǎn)系統(tǒng)，假設(shè)沒有兩點(diǎn)發(fā)生過碰撞，請找出各點(diǎn)坐標(biāo)在已知時(shí)間函數(shù)中的序列展開，在任意時(shí)間段內(nèi)均勻收斂。

翻譯一下就是：太陽系穩(wěn)定嗎？會(huì)把我們的地球甩出去嗎？

時(shí)年29歲的法國數(shù)學(xué)家龐加萊接受了這一挑戰(zhàn)。二體問題此前已被牛頓解決，于是龐加萊從限定條件下的三體問題入手：

假設(shè)其中兩個(gè)質(zhì)點(diǎn)的質(zhì)量足夠大，使得第三個(gè)質(zhì)點(diǎn)的質(zhì)量對前兩個(gè)不造成影響（有點(diǎn)像是研究兩個(gè)行星和一粒灰塵之間的相互作用）。

這還不夠，再把它們的運(yùn)動(dòng)都限制在同一個(gè)平面上。

△龐加萊手稿

怎么樣，夠簡化了吧。

可是龐加萊用了整整三年時(shí)間也沒得出完整結(jié)果，只是解出了一些特殊情況。最后趕在大賽截止日期前提交了論文，還成功勝出，領(lǐng)到了獎(jiǎng)金，美滋滋。

△龐加萊

然而在論文出版之前，審稿人對論文的某一部分看不太明白，寫信向龐加萊請教。

龐加萊細(xì)化自己的論證時(shí)，卻發(fā)現(xiàn)了致命錯(cuò)誤，趕緊聯(lián)系出版社撤回已經(jīng)印刷的論文，又把獎(jiǎng)金全賠進(jìn)去了。

在修訂論文的過程中，龐加萊發(fā)現(xiàn)了三體系統(tǒng)對初始條件的敏感依賴性。

即使完全知道了運(yùn)動(dòng)的規(guī)律，初始條件的細(xì)微差別，有時(shí)也會(huì)造成系統(tǒng)隨后運(yùn)動(dòng)的極大不同，使長期預(yù)測變得不可能。

這個(gè)現(xiàn)象后來被稱為混沌。

這就是《三體》小說中三體人面臨的生存難題了——

在那個(gè)世界中，太陽有3個(gè)。

由于三個(gè)太陽運(yùn)動(dòng)軌跡的混沌性，三體人會(huì)遭遇晝夜季節(jié)無規(guī)律更替的“亂紀(jì)元”，極端天氣帶來嚴(yán)苛的生存環(huán)境讓三體文明不斷地毀滅。

現(xiàn)實(shí)地球上的天氣變化雖然沒那么危險(xiǎn)，但也是混沌系統(tǒng)。

氣象學(xué)家洛倫茲用“蝴蝶效應(yīng)”來解釋這種現(xiàn)象，即蝴蝶扇動(dòng)翅膀造成初始條件的微小差異，經(jīng)過時(shí)間的放大都會(huì)造成劇烈的變化。

后來，有了計(jì)算機(jī)的幫助，科學(xué)家們能夠計(jì)算出更多三體問題中，一些存在周期性的特殊解。

如2017年，來自上海交大的研究團(tuán)隊(duì)就利用超級(jí)計(jì)算機(jī)，一口氣發(fā)現(xiàn)了600多個(gè)全新的周期解。

但三體問題的通用解，還籠罩在混沌的陰影下。

這次做出了什么突破？

既然是混沌系統(tǒng)，那就沒辦法了。

但并不意味著“三體系統(tǒng)”就研究不了——

這不，還有統(tǒng)計(jì)學(xué)嘛。

統(tǒng)計(jì)力學(xué)的著名科學(xué)家路德維希·玻爾茲曼，在1871年曾經(jīng)提出過一個(gè)假說：

各態(tài)歷經(jīng)假說(ergodic hypothesis)：一個(gè)孤立系統(tǒng)從任一初態(tài)出發(fā)，經(jīng)過足夠長的時(shí)間后，將經(jīng)歷一切可能的微觀狀態(tài)。

△雙擺系統(tǒng)，混沌系統(tǒng)之一

孤立系統(tǒng)，從熱力學(xué)角度來說，指不與外界交換能量或質(zhì)量的系統(tǒng)。

只要時(shí)間夠長，這種系統(tǒng)中所有可能的狀態(tài)都會(huì)發(fā)生。

在這個(gè)前提下，加上計(jì)算機(jī)和計(jì)算物理學(xué)的發(fā)展，蘇聯(lián)科學(xué)家在20世紀(jì)60年代有了新的突破。

對于由質(zhì)量無等級(jí)差距的三個(gè)物體形成的“非層級(jí)三體系統(tǒng)”，有一個(gè)狀態(tài)是最可能發(fā)生的——

其中一個(gè)體最終會(huì)逃逸出去，另外兩個(gè)演變成規(guī)律運(yùn)動(dòng)、可預(yù)測的“雙星”系統(tǒng)。這個(gè)過程被稱作三體系統(tǒng)的衰變(Decay)。

△就像這樣

不禁讓人想到這個(gè)場景……（手動(dòng)狗頭）

就這樣，研究的目標(biāo)變成了“三體問題的統(tǒng)計(jì)預(yù)測是怎樣的”。

之后的研究發(fā)展并完善了使用相空間(Phase Space)來描述三體系統(tǒng)狀態(tài)的方法。(相空間是一個(gè)假想的空間，系統(tǒng)每個(gè)可能的狀態(tài)都對應(yīng)相空間中的一個(gè)點(diǎn))

時(shí)間來到2019年，來自希伯來大學(xué)的Nicholas Stone等人，終于在此基礎(chǔ)上得出了非層級(jí)三體問題的統(tǒng)計(jì)學(xué)閉合解。

然而，這項(xiàng)研究還有一些瑕疵。

按照牛頓的理論，引力是無距離限制的。導(dǎo)致描述三體系統(tǒng)狀態(tài)的相空間的體積也是無限的。

Stone團(tuán)隊(duì)人為假設(shè)了一個(gè)“強(qiáng)相互作用區(qū)域”來解決這個(gè)問題。

還有，用相空間體積來確定概率，從而忽略了相空間的相當(dāng)一部分區(qū)域描述的是有規(guī)律、可預(yù)測的運(yùn)動(dòng)情況，其中包括系統(tǒng)衰變后剩下二體的運(yùn)動(dòng)。

△特定初始條件下的規(guī)則運(yùn)動(dòng)

同樣來自希伯來大學(xué)的物理教授Barak Kol，將研究對象聚焦在系統(tǒng)衰變時(shí)相空間的流出通量(Outgoing Flux)上，而不是相空間本身。

這樣即使相空間是無限的，其通量也是有限的，就無需引入假設(shè)的強(qiáng)相互作用區(qū)域了。

Kol團(tuán)隊(duì)還補(bǔ)充了統(tǒng)計(jì)演化模型來計(jì)算系統(tǒng)衰變，可以呈現(xiàn)為下面這張管道圖。

從圖中來看，三體系統(tǒng)的運(yùn)動(dòng)狀態(tài)可以分成兩種，規(guī)則(regular)和遍歷(ergodic)，其中遍歷的情況要明顯多于前者。

而逃逸的情況，也同樣分成兩種，逃逸(escape)和偏移(sub-escape)。

Kol團(tuán)隊(duì)把三體系統(tǒng)的狀態(tài)變化類比成在一個(gè)有光滑反射壁和一個(gè)小孔的瓶子里不斷反射。

在經(jīng)過一段時(shí)間后，從小孔脫離遍歷的系統(tǒng)狀態(tài)會(huì)進(jìn)入“逃逸”或是“偏移”。

用這種統(tǒng)計(jì)方法預(yù)測的質(zhì)點(diǎn)逃逸概率，比2019年和2006年的兩項(xiàng)研究所做的統(tǒng)計(jì)預(yù)測，都要更接近數(shù)值模擬值。

下圖是三個(gè)“三體”星系的質(zhì)量，以及它們逃逸的概率預(yù)測(其中M☉是太陽質(zhì)量，約為2×103o千克)。

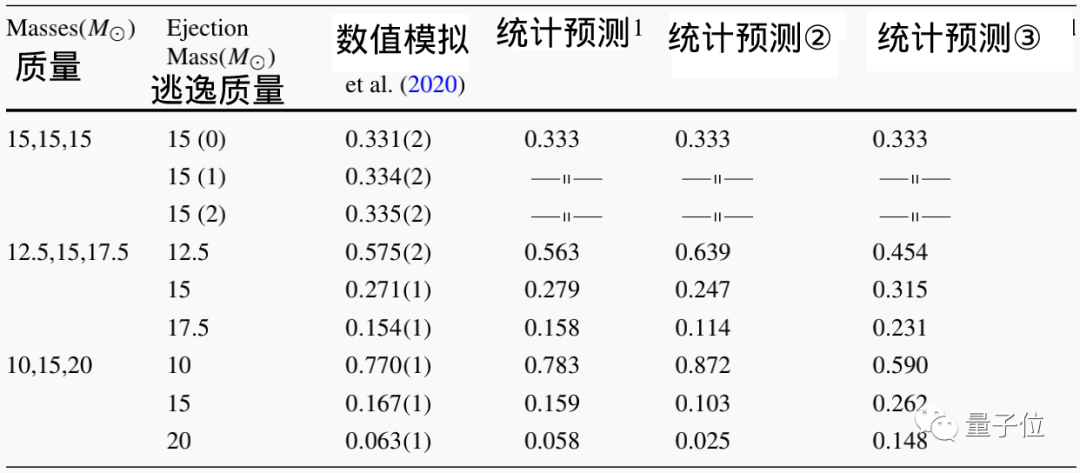
其中，“統(tǒng)計(jì)預(yù)測1”是這次研究的預(yù)測結(jié)果。

從圖中可見，相比于其他兩項(xiàng)最新研究，這一研究的統(tǒng)計(jì)預(yù)測結(jié)果，都更加貼合用“數(shù)值模擬”計(jì)算所得到的質(zhì)點(diǎn)逃逸率。

當(dāng)然，從圖中也能看出，質(zhì)量更小的質(zhì)點(diǎn)更容易發(fā)生“逃逸”情況。

對于這項(xiàng)研究給出的統(tǒng)計(jì)方法，論文作者、物理教授Barak Kol表示：

在數(shù)百萬臺(tái)計(jì)算機(jī)上進(jìn)行的模擬測試表明，這一理論所計(jì)算的結(jié)果，和計(jì)算機(jī)模擬的結(jié)果高度符合。

希伯來大學(xué)出品

這次的論文作者Barak Kol，是以色列希伯來大學(xué)的一名物理教授，曾于斯坦福大學(xué)獲得物理博士學(xué)位，還在特拉維夫大學(xué)、普林斯頓大學(xué)從事過博士后工作。

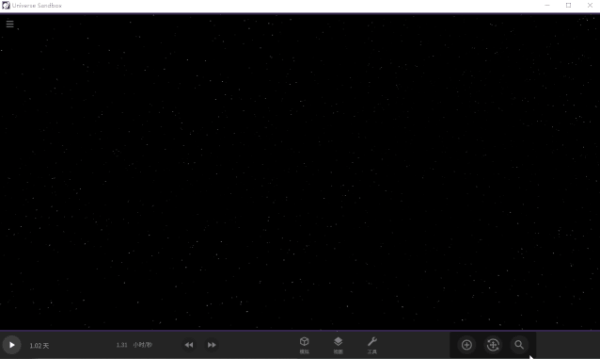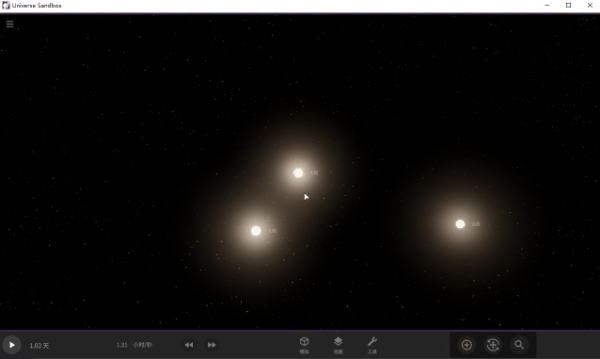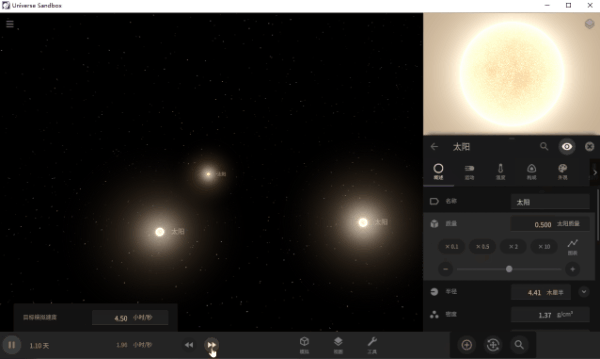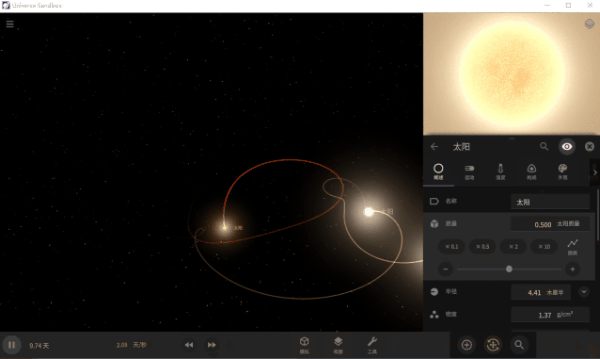
PS，如果想要自己制作“三體”模擬動(dòng)畫的話，還可以用文末的Universal Sandbox游戲試試~

可在任意位置添加天體，并修改質(zhì)量、體積等屬性，然后觀察運(yùn)動(dòng)軌跡。

論文地址：

https://link.springer.com/article/10.1007/s10569-021-10015-x

上海交大600個(gè)三體特殊解動(dòng)畫：

http://numericaltank.sjtu.edu.cn/three-body/three-body-movies.htm

Universal Sandbox：

https://store.steampowered.com/app/230290/Universe_Sandbox/

參考鏈接：

[1]http://www.mittag-leffler.se/library/henri-poincare

[2]https://mathematica.stackexchange.com/questions/135857/jacobian-of-parametricndsolve-and-findroot-for-the-three-body-problem

[3]https://phys.org/news/2021-y-theory-centuries-old-physics-problem.html

[4]https://nature.com/articles/s41586-019-1833-8

[5]https://arxiv.org/abs/2101.03661

（聲明：本文僅代表作者觀點(diǎn)，不代表新浪網(wǎng)立場。）