來源：原理

　　圓，是我們生活中最常見的形狀。神奇的是，無論一個圓是像星球般大小，還是比原子更小，圓的周長與直徑之比總是等于π（約等于3.14）。無論是在生活中，還是在揭開宇宙最深層次奧秘的公式中，我們都可以看到這一神奇的常數(shù)。

　　1、π的萊布尼茨公式  

　　等式右邊展開的無窮級數(shù)被稱為萊布尼茨級數(shù)，或馬達瓦級數(shù)。這個無窮的交替級數(shù)會收斂到π/4，它是逆正切函數(shù)展開式的一個特例，最早由印度數(shù)學家馬達瓦于14世紀發(fā)現(xiàn)，并在17世紀70年代由萊布尼茨首次發(fā)表。仔細觀察就能發(fā)現(xiàn)，這個公式將所有奇數(shù)與圓周率聯(lián)系在一起，因此它也將數(shù)論與圓和幾何聯(lián)系了起來。通過這種方式，π連接了兩個看似獨立的數(shù)學世界。

　　2、巴塞爾問題  

　　1+1/4+1/9+1/16+。。。這個無窮級數(shù)的求和問題被稱為巴塞爾問題，它至少在1644年時就已經(jīng)存在。幾位著名的數(shù)學家都研究過這個問題，包括萊布尼茲，但他并沒有找到精確解。直到1735年，歐拉精確地計算出了所有平方數(shù)（即1=12，4=22，9=32，16=42。。。）的倒數(shù)之和。

　　3、歐拉恒等式  

　　歐拉恒等式聯(lián)系了數(shù)學中最基本的五個數(shù)字，它被比作是莎士比亞的十四行詩，在許多人心中，這無疑是“最美公式”。

　　4、雙曲幾何中的三角形面積  

　　雙曲幾何是非歐幾里得幾何的一種特例。它的一項顯著的性質(zhì)是，其三角形的內(nèi)角α、β、γ之和總是小于180o。在幾乎同一時間，俄國數(shù)學家巴羅切夫斯基與匈牙利數(shù)學家鮑耶發(fā)現(xiàn)，雙曲幾何中的三角形的面積可以通過π與內(nèi)角和之差求得。

　　5、高斯-博內(nèi)定理  

　　高斯-博內(nèi)定理是曲面微分幾何中意義最為深遠的結(jié)果之一，它是拓撲和微分幾何之間的橋梁。它表明，閉合曲面的總曲率只與它的拓撲有關(guān)。該定理產(chǎn)生了各種各樣強大的應(yīng)用。

　　6、等周不等式  

　　等周不等式也被稱為等周定理，是幾何中的一個不等式定理，它將歐幾里得平面上的閉合曲線的邊界長度l（周長）與其包圍的面積A聯(lián)系了起來。在所有閉合曲線所形成的形狀中，圓形的面積最大，僅在此時等號成立。

　　7、π的倒數(shù)的無窮和表達式  

　　與歐拉恒等式不同，拉馬努金推導的這一極其復雜、繁繞的以無窮和的形式表達的π的倒數(shù)常被許多數(shù)學家調(diào)侃為“最丑”的數(shù)學公式。

　　8、愛因斯坦場方程  

　　這一方程是愛因斯坦在1915年提出的廣義相對論的核心方程。它說的是：引力 = 比例常數(shù) ×（能量與動量）。簡而言之，廣義相對論可以總結(jié)為：時空決定了物質(zhì)如何運動，物質(zhì)決定了時空如何彎曲。

　　9、不確定性原理  

　　海森堡的不確定性原理是量子力學的一個重要原理。粗略地說，它闡述的是我們無法同時絕對確切地知道一個粒子的位置和動量，其中一個屬性被測量得越準確，對另一個的了解就越不準。但這一原理可延伸到粒子的其他某些物理屬性對（被稱為互補變量），例如時間長度和能量之間的關(guān)系也是以類似的不等式表示的。

　　10、黑洞溫度  

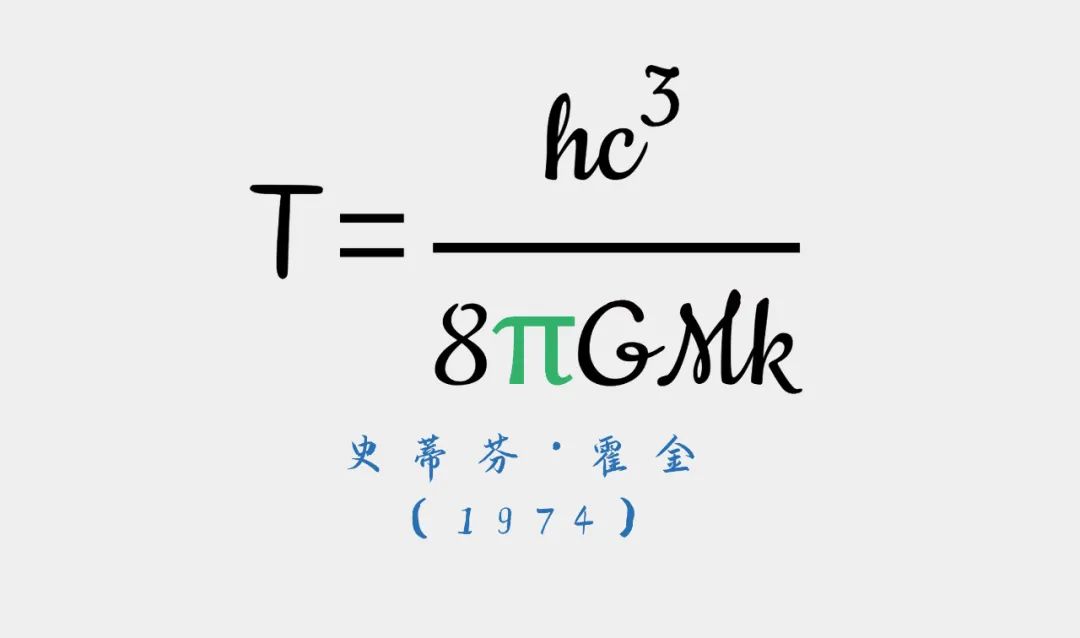
　　霍金在運用量子力學研究了黑洞鄰近彎曲時空中的粒子后發(fā)現(xiàn)，黑洞具有溫度（T）。而就像所有具有溫度的物體一樣，黑洞也能產(chǎn)生輻射，這種現(xiàn)象被稱為霍金輻射。這一公式包含了牛頓的萬有引力常數(shù)（G）、普朗克常數(shù)（h）、光速（c）、以及玻爾茲曼常數(shù)（k）。也就是說，霍金的工作把量子理論、廣義相對論和熱力學全部聯(lián)系在了一起。

　　#創(chuàng)作團隊：

　　撰文：原原

　　排版：雯雯

　　#圖片來源：

　　封面圖：NASA/JPL-Caltech

　　首圖：NASA/JPL-Caltech