來源：原點閱讀

　　編輯：云開葉落

　　考屆一直流傳著這樣一個傳說，“不會就選C”據說被歷代學子們奉為不會做題時答題“上策”。

　　你有沒在考試中遇到選擇題拿不準答案就選了C，然后就蒙對了的經歷？

　　標準化考試是國際上廣為流行的考試方法，它具有客觀性強，覆蓋面廣，評卷迅速等優點。選擇題是標準化考試中最常采用的題型，我們在各種考試中都經常能見到選擇題的身影。

　　從題目的結構看，一般分為兩部分：一部分是提出或陳述一個問題，另一部分是備選答案，包含一個正確答案及幾個錯誤答案。我們來看下面的例子：

　　[選擇題]以下圖形中有幾個是正方體的表面展開圖？

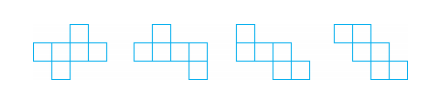
　　A.1個；B.2個；C.3個；D.4個。例子中備選答案有4個，只有D項是正確的。

　　一道選擇題的備選答案數，我們稱為“項數”。上面的例是一道4項選擇題。雖然選擇題作為考試的題型，有著許多優點，但也存在一個嚴重的不足，即難于摒棄“碰運氣”的成分。具體地說，對一個一無所知的人來說，單憑機遇也可能碰上幾個正確的答案。

　　事實上，一道λ項的選擇題，隨機選取恰好碰上正確答案的概率是1/λ，碰到不正確答案的概率是1-（1/λ）。假設共有n 道這樣的選擇題，光憑機遇隨機選對k題的概率為

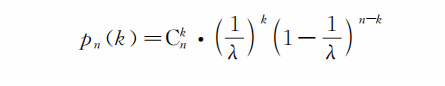
　　具體些，如果我們有10道題，每道題有4個備選答案，即 n=10，λ=4。

　　那么，可以一個個算出隨機選對k題的概率（只是相應的

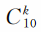
　　要從楊輝三角的第10排去查），列表如下。

　　隨機選題概率 

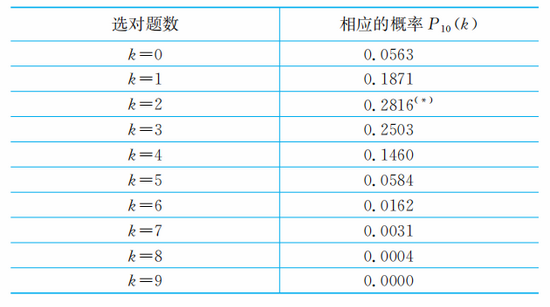
　　從表中容易看出，光憑機遇選對兩道題或三道題的可能性占了過半，如果這也“給分”的話，顯然是不夠合理的。正是由于存在這種不合理性，所以許多國家的考試組織者，都對各種考試做了形式各異的彌補性規定。

　　如美國中學數學競賽，共有30道選擇題，每卷給30分基本分，以平衡隨機得分。只有全錯才得0分， 但全錯的可能性是極少的。

　　又如我國有些數學聯賽試題，對選擇題得分做如下規定：答對得滿分，答錯得0分， 不答得1分。這主要是鼓勵學生“知之為知之，不知為不知”，不要去做碰運氣選題的事。再如2013年蘇州大學的自主招生，語文、數學、物理、化學的考試試題均由40道選擇題組成，得分規定為：選對的得5分；不選的得0分；選錯的扣2分。這里設置的扣分，意在懲罰那些碰運氣的人。

　　上面的眾多規定，既有合理的一面，也都有不合理的地方。從科學的角度看，要讓那些靠碰運氣選題的人得不到分，才算合理。為此，我們必須去求靠碰運氣最可能會選對的題數k* ，這相當于解以下不等式組：

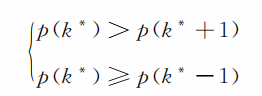
　　僅限于初中的知識，要解上面不等式組還有一定困難，但解得的結果卻是很簡單的： 

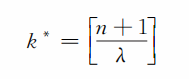
　　其中[x]表示不超過x 的最大整數。如[π]=3，[lg32]=1等。在前面例中 

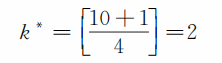
　　這與表中查到的相應概率的最大值是一致的。當k* 確定之后，我們便可以設置扣分，使得選對k* 題的人得不到分。科學的扣分法有兩種。

　　第一種方法： 

　　設答對一道題得r分，答錯一道題得0分，每卷以-k*r為基本分，且總得分不取負值。顯然，全對者得（n-k* ）r，即為滿分。如前例中的10道題，假定每道題答對得5分，由于k* =2，所以基本分可定為-2×5=-10分，滿分為40分。 

　　第二種方法： 

　　設答對一道題得r分，答錯一道題扣t分，基本分為0分。t的選取，要使選對k* 題的人得不到分數（因為我們認為他是純粹靠運氣選對的）。因此，該卷所得分數應與所扣分數相當， 即k*r=（n-k* ）t，算得 

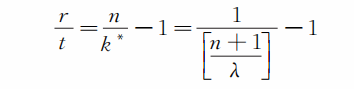
　　對于多項選擇題，隨著項數λ 的增大，靠機遇選對的題數 k* 相應減少。對于這種情形，即使不設置扣分，也不至于對總分造成過大的影響。

　　從k* 的計算式可以看出，要減少k* 的途徑有兩條，一是減少題目數量，二是增大項數。減少題目的數量是沒有實際意義的，而增大備選答案的個數，又對設計題目造成了困難。怎么辦呢？最近，有的考試采用了一種叫作“多解選擇”的辦法，每個備選答案都可能是正確的或錯誤的（與單一選擇的區別是，不再只有一個答案正確）。這樣，λ 個備選答案，每個答案都有“取”與“不取”兩種選擇，共有

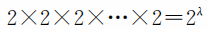
　　種選取的方法。除去都不選的一種情形，實際項數有 

　　這顯然比單一選項的項數要高得多。例如，備選答案只有3個的多解選擇，實際項數

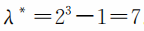
　　項數這樣高，隨機選對的可能性勢必很小。因而，多解選擇一般是沒有必要去設置扣分的。