基于GARCH族模型的VaR與CVaR值的實證研究(3)
4.3 ECM模型
誤差修正模型的結果如下:
表5、股票組合收益率與HS300股指期貨收益率的誤差修正模型
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
-0.000270 |
0.001410 |
-0.191680 |
0.8484 |
|
GPZH(-1) |
0.1 7921 2 |
0.098233 |
1.824354 |
0.0712 |
|
HS300 |
0.969253 |
0.047796 |
20.27909 |
0.0000 |
|
HS300(-1) |
-0.315882 |
0.10 5787 |
-2.986034 |
0.0036 |
|
R-squared |
0.823281 |
Mean dependent var |
-0.001979 |
|
|
Adjusted R-squared |
0.817700 |
S.D. dependent var |
0.032687 |
|
|
S.E. of regre ss ion |
0.013956 |
Akaike info criterion |
-5.666213 |
|
|
Sum squared resid |
0.01 8504 |
Schwarz criterion |
-5.561360 |
|
|
Log likelihood |
284.4775 |
F-statistic |
147.5254 |
|
|
Durbin-Watson stat |
2.079251 |
Prob(F-statistic) |
0.000000 |
|
4.4 GARCH模型
我們對2005年1月4日至2008年8月日的數(shù)據(jù)進行檢驗,LM檢驗的P值均大于0.05,因此,收益率序列的隨機擾動項呈現(xiàn)波動集群性的特征,而且殘差存在高階ARCH效應,我們利用GARCH(1,1)模型來刻畫這種效應。
表6、GARCH模型
|
|
Coefficient |
Std. Error |
z-Statistic |
Prob. |
|
HS300 |
0.977398 |
0.050874 |
19. 2120 6 |
0.0000 |
|
|
Variance Equation |
|||
|
C |
1.29E-05 |
2.29E-07 |
56.45598 |
0.0000 |
|
ARCH(1) |
-0.125718 |
0.072972 |
-1.722838 |
0.0849 |
|
GARCH(1) |
1.07 2168 |
0.067209 |
15.95265 |
0.0000 |
|
R-squared |
0.799614 |
Mean dependent var |
-0.001962 |
|
|
Adjusted R-squared |
0.793352 |
S.D. dependent var |
0.032522 |
|
|
S.E. of regre ss ion |
0.014784 |
Akaike info criterion |
-5.650477 |
|
|
Sum squared resid |
0.020982 |
Schwarz criterion |
-5.546271 |
|
|
Log likelihood |
286.5239 |
Durbin-Watson stat |
1.634452 |
|
4.5 不同模型估計的避險比率的比較:確定最優(yōu)套保比率
我們發(fā)現(xiàn)ECM模型套保效率較高,據(jù)此,我們確定最佳套保比率為:0.9568
表7、不同模型計算出的套保比率和套保效率HE
|
觀察估計期 |
方法 |
套保比率 HR |
避險期 |
避險期方差 |
套保效率 HE |
|
未套保 |
0 |
0.000561 |
- |
||
|
100 個交易日 |
OLS |
0.9722 |
5 個交易日 |
0.000057 |
0.898 |
|
(071217-080519) |
ECM |
0.9568 |
(080520-080526) |
0.000055 |
0.903 |
|
GARCH |
0.9774 |
0.000058 |
0.896 |
4.6 計算交易需要的期貨合約數(shù)量
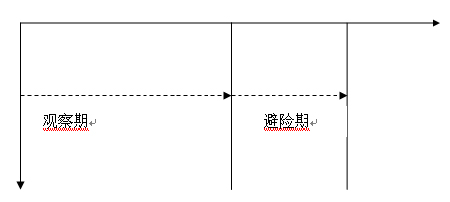
圖2:觀察期與避險期示意圖
2008年4月18日該私募基金持有的投資組合市值為1209.43萬,持有到5月19日,市值增至1371.94萬,該基金經理判斷市場未來會下跌,以19日的收盤價(我們以5月19日滬深300指數(shù)點位3914.07替代當時的股指期貨價格)賣出股指期貨合約進行賣出套期保值,根據(jù)前面計算出來的期貨合約的數(shù)量:
根據(jù)套保流程給出的建議,我們對期貨合約數(shù)量的零數(shù)進行返算優(yōu)化處理。即用計算出的合約數(shù)量的整數(shù)及整數(shù)+1 分別返算套保比率HR 和套保效率HE,分別得到兩個HR 和HE,選擇較佳的套保效率HE 對應的期貨合約整數(shù)數(shù)量。我們分別以11和12返算得出的套保比率和套保效率如下表所示:
表8、返回優(yōu)化處理表
|
返回的期貨合約數(shù)量 |
套保比率 HR |
套保效率 HE |
|
11 |
1.0622 |
0.8574 |
|
12 |
0.9737 |
0.8973 |
根據(jù)返算優(yōu)化的處理方法,我們選擇最佳套保效率HE 對應的期貨合約數(shù)量,得到需交易的期貨合約數(shù)量=12 份。
4.7 套期保值的盈虧分析
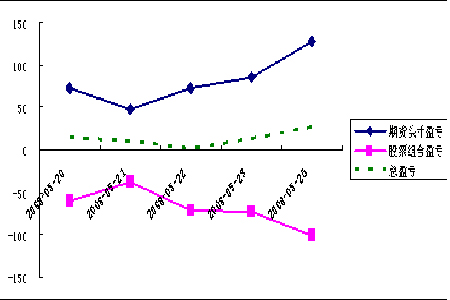
私募集基金經理執(zhí)行本次套期保值策略的盈虧情況見表9,不同交易日現(xiàn)貨期貨部頭盈虧狀況見圖3。從表7可以看出,選擇套保比率0.9568,期貨合約份數(shù)12 進行套期保值效果較好。在避險期內期貨頭寸盈利127.75萬元,現(xiàn)貨頭寸損失101.08萬元,期貨盈利能完全彌補現(xiàn)貨損失,套期保值效果顯著。在本案例中,從圖3中可以看出,基差并沒有走強(圖3所示),之所以盈利,是因為選用12張期貨合約>11.1796,從此案例中仍然存在基差走弱的風險,只不過是被多余的期貨頭寸給抵消掉了。
表9、套期保值盈虧分析表
|
|
股票組合 |
股指期貨 |
|
2008-5-19 |
1371.94 |
3914.07 |
|
2008-5-26 |
1270.86 |
3559.21 |
|
盈虧 |
-101.080 (萬) |
127.750 (萬) |
圖3:套保期間股票組合市值與滬深300
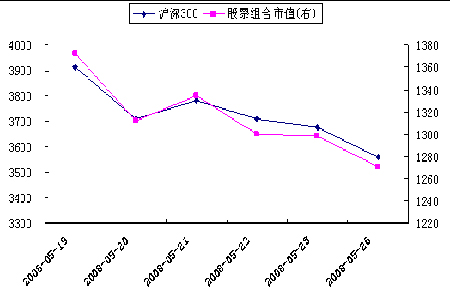
圖4:賣出套期保值總盈虧示意圖
宏源期貨 馬春陽、劉健、宋寧笛
新浪聲明:此消息系轉載自新浪合作媒體,新浪網登載此文出于傳遞更多信息之目的,并不意味著贊同其觀點或證實其描述。文章內容僅供參考,不構成投資建議。投資者據(jù)此操作,風險自擔。