5.3 GARCH模型的建立

　　下面我們將基于GARCH(1,1)模型的動態跨期套利策略對ln(kmh9)和ln(kmm9)之間的關系進行擬合，結果如下：

　　對殘差序列resid01進行ARCH LM檢驗，檢驗結果為：

ARCH Test:
F-statistic	0.763055	Probability	0.466788
Obs*R-squared	1.530640	Probability	0.465185

　　資料來源：光大證券研究所

　　此處P=0.467，表明在對其殘差建立GARCH(1,1)模型后，ARCH效應消失了，且表明GARCH(1,1)能很好的捕捉殘差中的波動叢集性。

　　將GARCH(1,1)模型的結果代入樣本外數據：

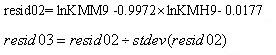
　　5.4 交易策略及結果

　　圖表3  resid03的分布圖            

圖為resid03的分布圖。（圖片來源：光大證券研究所）點擊此處查看全部財經新聞圖片

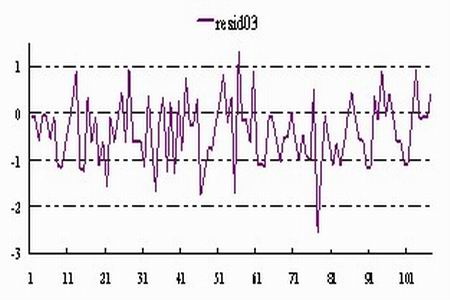
　　圖表4  resid02的分布圖

圖為resid02的分布圖。（圖片來源：光大證券研究所）點擊此處查看全部財經新聞圖片

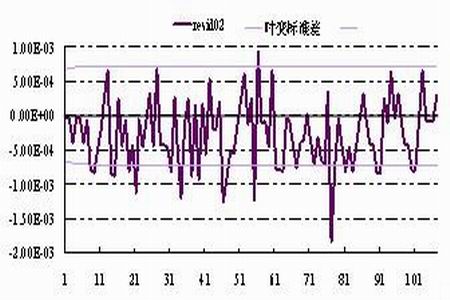
　　我們采取的交易策略為：

　　交易結果為：

類別	策略效果
套利交易次數	18
套利成功次數	18
套利時間占全部交易時間比例	25.2%
成功次數占交易次數比例	100%
單筆交易最大盈利	66741
總盈利	800999
平均每筆盈利	44499.94

　　資料來源：光大證券研究所

　　從實證結果看，套利交易次數占全部交易日的比例在20%以上，單次套利交易的獲益水平在45000韓元之間，以單次套利投入資金2200萬韓元計算，單次套利交易的收益率水平在0.2%附近。

　　5.5 與傳統方法比較

　　根據持有成本理論的套利價差空間的效果，在持有成本理論套利分析中，假設：

　　圖表5  持有成本理論的基差分布圖

圖為持有成本理論的基差分布圖。（圖片來源：光大證券研究所）點擊此處查看全部財經新聞圖片

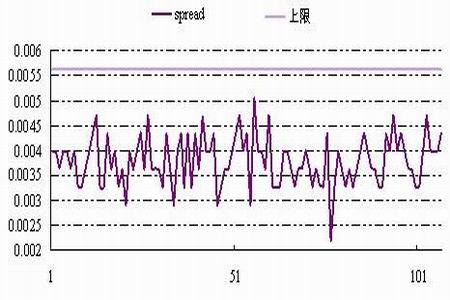
　　由圖可知，spread一直處于無套利空間，一次套利機會都沒有，在同樣的樣本外數據內，基于GARCH模型的跨期套利次數為18次，成功率100%，明顯優于基于成本理論的套利效果。由此可見，基于GARCH模型的跨期套利策略大大提高了同時段套利機會的次數和效率。

　　6. 總結

　　我們利用GARCH模型研究股指期貨合約的跨期套利，其實這是一種統計套利，是估計兩個不同交割月份的股指期貨合約之間的合理價差進行的套利交易。該方法有別于純粹對賭近期和遠期合約走勢的投機套利交易行為，為股指期貨跨期套利提供了一種新的思路和方法。

　　本文中可以看到，韓國股指期貨的跨期套利機會較多，跨期套利收益相對豐厚，出現套利機會的頻率較高，但同時也存在的一個問題：模型中的 并不為一整數，而在現實交易中只能做整數合約的交易，在這里可以將多余的非整數部分用ETF或成份股的組合來對沖。

　　光大證券研究所 于棟華

    新浪聲明：新浪網登載此文出于傳遞更多信息之目的，并不意味著贊同其觀點或證實其描述。文章內容僅供參考，不構成投資建議。投資者據此操作，風險自擔。